Unity中实现Volumetric Fog
Theory
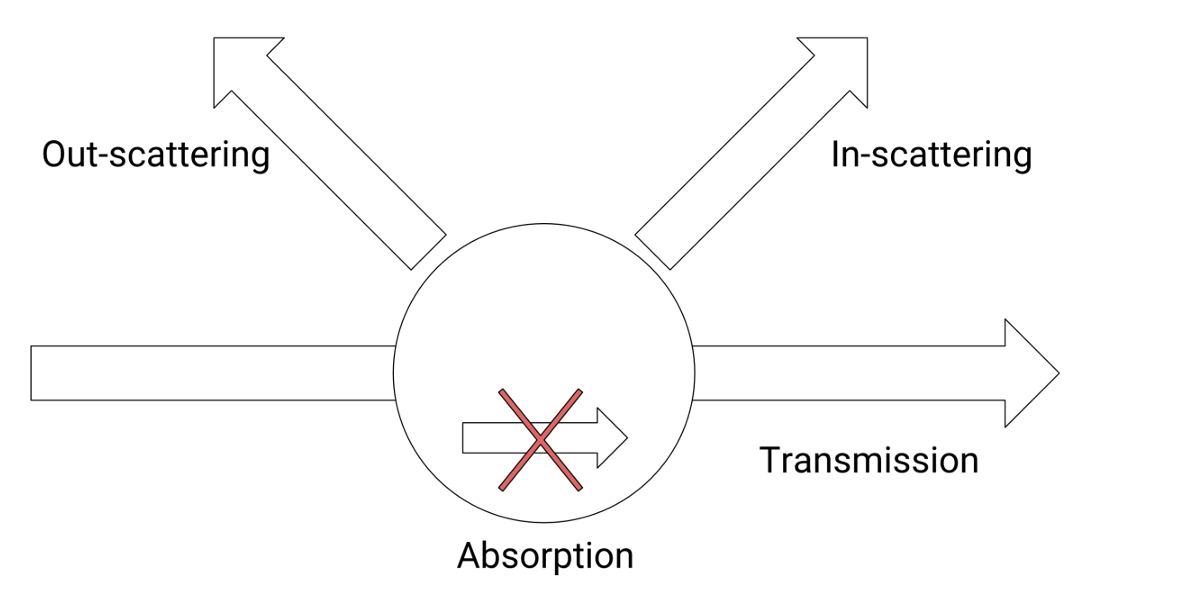
显然我们无法模拟每个组成雾的粒子，但是我们尝试计算可一个较小空间中雾粒子的密度，然后根据密度值来计算粒子与光源的交互，也就是transmission、absorption、scattering。
如下图所示，当光线进入一个体积时，会发生以下几种情况：
- out-scattering：将光线散射回光源所在的方向
- in-scattering：将光线散射到相机所在的方向
- absorption：光线与组成雾的粒子交互所损失的能量
- transmite：光线在雾中的透射
我们可以用数学表达式描述这一过程：
\[L_{\text{transmittance}} = L_{\text{incoming}}-L_{\text{absorptoin}}-L_{\text{scatter}}\]大气散射
大气的散射作用对于不同波长的光线的影响是不同的：波长越短，则受到的散射越强。波长短的光线的颜色较冷，这也是为什么晴朗的天空呈现蓝色。影响短波长的散射通常是Rayleigh散射。
在计算机图形学中，我们是用相位函数来描述光线在散射过程中的方向分布。Rayleigh散射对应的相位函数的数学表达式为：
\[p(\theta, g)=\frac{3*(1+cos^2(\theta))}{16\pi}\]其中，$\theta$表示光线方向与视线方向之间的夹角，$g$作为雾的各向异性参数，范围在$[-1, 1]$之间。雾倾向于向一个受限的方向散射光线，我们称这个性质为雾的各向异性。
除了Rayleigh散射，还有一个Mie散射，后者倾向于散射具有更长波长的光线。在渲染领域中，我们通常使用Henyey-Greenstein相位函数来近似Mie散射：
\[p(\theta, g)= \frac{1-g^2}{4\pi * (1+g^2-2*g*cos(\theta))^{3/2}}\]但是Henyey-Greenstein相位函数也存在一个缺点，也就是没有考虑到对于微小颗粒在光照下的散射特性。我们可以考虑使用Cornette-Shanks相位函数，它与Henyey-Greenstein相位函数具有相似的形式，但是在物理上更正确，它的数学表达式如下：
\[p(\theta, g)=\frac{3(1-g^2)(1+cos^2(\theta))}{2*(2+g^2-2*g*cos^2(\theta))^{3/2}}\]我们使用Beer-Lambert定律来计算入射光线的透射率。该定律指出，透射率与光线在volume中的行进距离成指数关系：
\[T(A\rightarrow B)=e^{-\int_A^B\beta e(x)dx}\]其中，$\beta e$是散射系数与吸收系数之和。
Volumetric Fog算法
体积雾效的算法可以分为五个步骤：
- 采样noise
- 采样shadow map
- 添加光照
- 对雾效应用模糊
- 将雾效合成到场景中
Noise
现实世界中的雾效几乎都具有非均一的密度。为了模拟这个特性，我们需要在渲染算法中引入noise函数。体积雾算法中所用的noise函数需要满足以下要求：
- deteministic：同一个输入值始终返回相同的结果
- continuous：返回的结果具有连续性
为了降低性能开销，我们可以将noise函数预先计算的结果存储在纹理，并加载到计算机内存中。通常来说，2D纹理所存储的值的范围是$[0, 1]$。当采样结果为1时，我们可以认为该点所对应的透射率为0。
Shadow Map
通过采样shadow map，我们可以判断volume中的某个点是否在阴影中。这一步对于实现体积光效果至关重要
Lighting
我们在这一步计算extinction、scattering、transmittance。
extinction对于volume中的每个位置都是一个常量，所以我们不妨乘以每个点的密度，构成一个新的参数参与体积计算。
scattering需要我们使用Cornette-Shanks相位函数与Payleigh相位函数的计算结果进行累计。
透射率则是对当前采样点应用Beer定律
Blur
现实世界中，光线在volume中行进时，部分光线会被散射到周围的介质中，从而使得雾效看起来变得模糊。同时Blur算法还承担着降噪的任务。
Composite
当算法执行到这一步时，体积雾的透射率存储在alpha通道中。透射率越低，则体积雾在对应采样点处的密度越大，使得该采样点处的几何体的可见性更低。
实现细节
Architecture
待补充
Raymarching
梳理坐标变换
先来看线性深度分布的情况