文章

URP中实现实时面光源

发表于 更新于
作者 褴褛飞旋
17 分钟阅读

1 Motivation

Cozy Space是一个装修模拟类游戏。它具有以下特点：

  • 灵活的房间户型设计：玩家可以构建任意的多边形房间
  • 时间/天气系统：玩家可以修改游戏中的时间段与天气，从而影响房间内的光照与氛围
  • 自由的家具摆放：玩家可以自由地摆放房间中的家具、装饰品

基于以下几点考虑，我最终选择使用实时面光源作为房间中的主要光照来源：

  • 平行光不适合作为封闭室内的照明来源，而更适合配合窗户和窗帘，营造室内氛围
  • 由于房间户型是相对任意的，对于较为复杂的房间（例如一个1x6的走廊），点光源和聚光灯无法提供较好的照明效果
  • 游戏中的所有家具都是可以自由拖放的，不存在静态对象，意味着不能使用光照烘焙等技术
  • 基于LTC的实时面光源技术能够配合PBR材质着色，与项目美术资产不冲突，能够实现高质量的室内照明

只是URP并没有实装可以实时面光源，所以我自己参考很多大佬的代码实现了一个能用的版本。

2 实现原理

2.1 Foundation of Area Lights

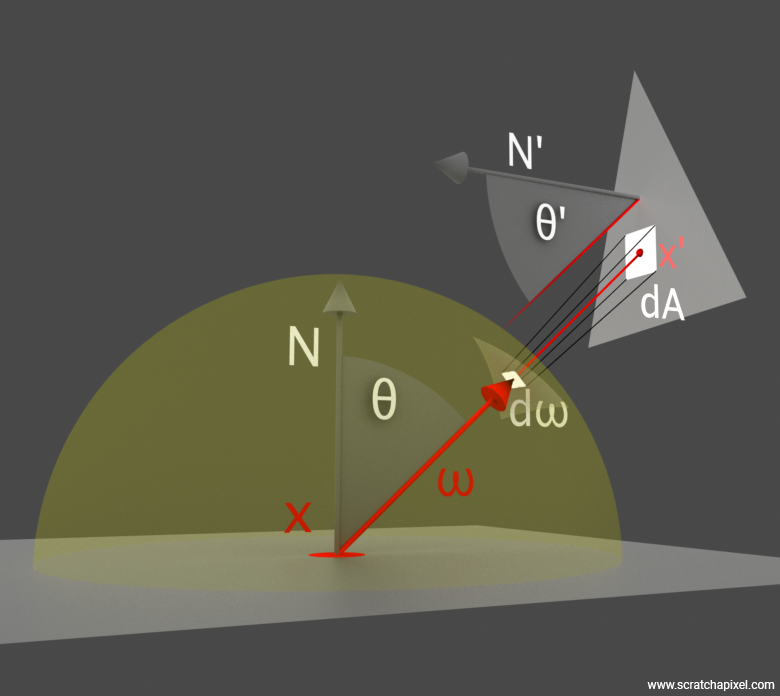
以法线为轴的半球空间囊括了所有有可能的入射方向，而我们需要对来自半球方向的光线进行积分，如下图所示，着色点的光照来源于两个区域光：

之所以面光源的光照计算构成了一个积分问题，是由于半球与面光源都是连续的表面，而非离散元素集合。面光源的渲染方程可以表述为：

\[L_o(\omega_o)=\int_{\Omega}L_e(\omega_i)\cdot f_r(\omega_i, \omega_o)\cdot V(\omega_i)\cdot cos\theta_i d\omega_i\]

在离线渲染中，积分可以通过蒙特卡洛方法解决，即在面光源表面均匀生成采样点。随后，将这些采样点与当前着色点连线，得到对应的光照方向向量。但既然我们需要在半球范围上进行积分，我们就需要建立起面光源表面上一点与半球所对应的立体角之间的对应关系。这里的思路是，将面光源投影到半球空间并在该区域采样。

这篇博客（虽然还没写完）详细讨论了面光源在离线渲染中的实现方法

2.2 Linearly Transformed Cosines

想要理解面光源的实时渲染，我们需要需要清楚地明白这几个问题：

  • 为什么离线渲染的方案无法应用在实时渲染中
  • LTC方案如何解决问题

我们依次来看

为什么离线渲染的方案无法应用在实时渲染中

主要处于以下两点原因：

  • 被积函数的高度非线性
    • 面光源积分需在立体角域内累加所有入射方向的 BRDF 贡献，而实时渲染中，BRDF（如 GGX）同时依赖与入射方向、观察方向和材质参数（粗糙度、金属度）
    • BRDF的计算包含了高次项与多变量的耦合，所以我们无法将其表示为输入变量的线性组合
    • 进而，我们无法解析求解，只能通过蒙特卡洛求数值解，这在实时渲染中中难以接受
  • 积分域动态变化：
    • 面光源的几何形状（如矩形的四个点）在半球空间的投影立体角$\Omega$会随观察方向和位置实时变化
    • 每次帧更新需重新计算积分域，传统方法（如预积分辐照度图）无法适应动态场景。

总结：积分太复杂了。

LTC方案如何解决问题

LTC方案的神奇之处在于，同时能够解决上述的两个问题：

  • 被积函数高度非线性

    • LTC 的核心假设是：任何各向同性 BRDF 可以通过线性变换近似为余弦分布。具体来说，针对不同粗糙度与观察方向，离线计算出一个3x3矩阵$M$，使得变换后的BRDF在规范空间内表现为简单的余弦分布。这一过程的数学形式为： \(f_r(\omega_i, \omega_o)\approx\frac{cos\theta'}{||M||}\) 其中，$\theta’$表示变换后的入射角。

    • 最终，被积函数中的复杂BRDF被替换为规范空间下的方向无关项$\cos\theta’$，消除了非线性

    • 而余弦分布的被积函数在规范空间中存在闭合解，无需蒙特卡洛采样

  • 积分域动态变化

    • LTC 将光源形状和观察方向动态变化的影响统一映射到规范空间

    • 具体来说，是通过逆矩阵$M^{-1}$将光源的角点从原空间变换到规范空间。其数学形式为： \(p_i'=M^{-1}\cdot(p_i-x)\) 其中：

      • $p_i$：原空间光源角点坐标
      • $x$：着色点坐标
      • $p_i’$: 规范空间下的光源角点坐标

    • 在规范空间内，光源形状（如矩形、圆盘）的积分域被转换为固定形状（如轴对齐矩形），其积分结果可通过解析公式直接计算。

    • 最终的结果是，无论光源位置、观察方向如何变化，只需实时计算 M−1 并变换光源角点，积分域的动态性被规范空间的固定性吸收。

2.3 变换矩阵$M$

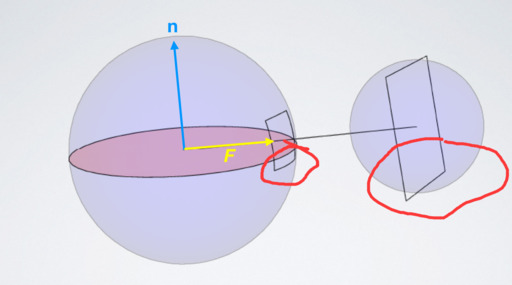
我们不难注意到，变换矩阵$M$是LTC方案的数学核心：通过线性变换$M$，能够将实际空间中的复杂BRDF与动态光源形状转换为规范空间内的余弦分布，从而使得面光源的渲染方程可以在实时条件下完成积分计算。

换句话说，余弦分布可以通过一个3x3的矩阵，变换到任意形状的球面分布，其中就包含BRDF的分布。

假设原空间的入射方向为$\omega_i$，规范空间的入射方向为$\omega_i’$，那么二者之间的变换关系为：

\[\omega_i'=M\cdot \omega_i\]

规范空间内的BRDF则被近似为：

\[f_r(\omega_i, \omega_o)\approx\frac{cos\theta'}{||M||}\]

实际上，矩阵$M$通过缩放、旋转和剪切操作，将原空间中 BRDF 的高光形状（如 GGX 的椭圆波瓣）扭曲为规范空间内的余弦分布。我们不妨分别分析一下矩阵$M$两个参数的影响：

  • 低粗糙度：BRDF 波瓣狭窄，M 表现为强烈的缩放（a→0,b→∞），将高光压缩到规范空间的法线附近。
  • 高粗糙度：BRDF 波瓣宽泛，M 接近单位矩阵（a→1,b→1），变换后接近原始余弦分布。
  • 正视角：BRDF 波瓣对称，M 为纯缩放矩阵
  • BRDF 波瓣拉长，M 引入剪切分量，以匹配高光的各向异性拉伸

最后，我们再了解一下M的构建方法。矩阵 M 的构建是一个离线优化问题，目标是最小化实际 BRDF 与余弦分布的差异。我们需要定义一个误差函数 E(M)，用于衡量变换后 BRDF 与余弦分布的差异。拟合的过程可以使用Nelder-Mead 算法。

2.4 光源角点的裁剪

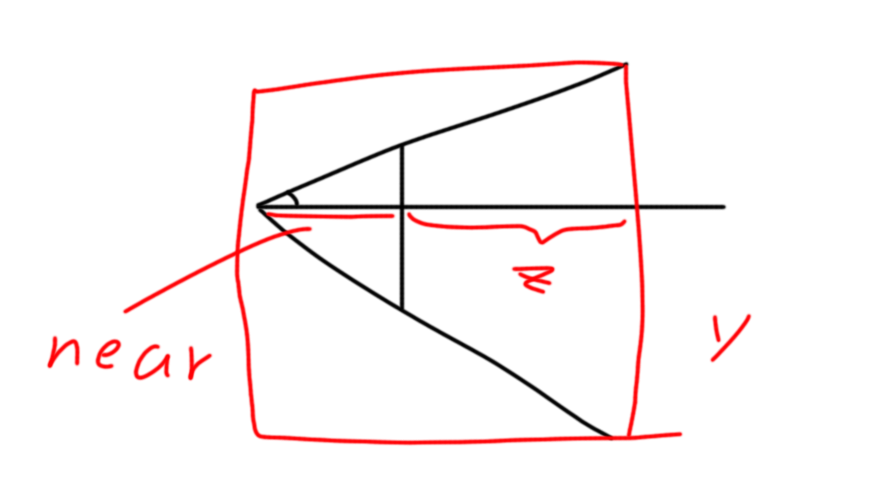
前面我们提到，通过矩阵$M$，我们将光源角点从实际空间变换到了规范空间，然而，规范空间中的光源可能部分位于单位半球外，需裁剪掉这些不可见部分，仅对半球内的光源部分进行辐照度积分。

所以，通过裁剪这个步骤，我们将变换到规范空间的光源顶点（如矩形光的四个角点），处理为多边形顶点序列（位于半球内或与半球边界相交）。

裁剪的具体算法相对来说不太复杂：

  1. 判断顶点可见性：即通过与法线的点乘，判断是否位于半球内
  2. 逐边裁剪：对光源多边形的每条边执行以下操作：
    • case 1：如果两端点均可见，即可保留该边，将两个顶点加入裁剪后的顶点列表
    • case 2：只有一端可见，此时需要计算边与半球的交点，然后将可见端点与交点加入列表
    • case 3：两点均不可见，直接剔除
  3. 计算边与半球的交点，构建参数方程，并将结果归一化到单位球面
  4. 去重：将顶点间距过小的点合并
  5. 闭合多边形
  6. 退化处理：若裁剪后的顶点数小于3，无法构成多边形，直接返回radiance为0。

2.5 余弦积分

当裁剪完成后，我们就可以计算余弦积分了，这也是LTC方案的最终目的，构建一个具有解析解的积分，一个可以在实时渲染中使用的积分。

在规范空间中，裁剪后的光源多边形radiance积分可以表示为：

\[L=L_e\cdot\frac{1}{||M||}\cdot\int_{\Omega'}cos\theta'd\omega'\]

而积分的本质在于，计算多边形区域在半球上的余弦加权立体角，即通过Stokes定理将面积分转换为边界积分，即，对单位球面上的多边形区域，其边界由一系列大圆弧组成，每条边的贡献与其夹角的符号相关，最终得到闭合解：

\[\int_{\Omega'}cos\theta'd\omega'=\sum_{i=0}^{n-1}\Phi(a_i, b_i)-(n-2)\pi\]

其中：

  • $a_i$与$b_i$表示裁剪后多边形的相邻顶点（已归一化到单位球面）
  • $n$表示裁剪后的顶点数
  • $\Phi(a, b)=arccos(a\cdot b)\cdot sign((a\times b)_z)$

最后，我们归纳一下余弦积分的实现方法：

  1. 计算每边的贡献：对裁剪后的多边形每条边，计算其夹角的弧度值，并根据边的缠绕方向确定符号。
  2. 累加贡献并修正曲率：累加所有边的符号化弧度值，减去 (n−2)π 修正球面几何误差。

2.6 LTC的实现步骤

既然我们已经有了一定的理论基础，现在不妨让我们再梳理一下LTC方案的具体实现步骤。

2.6.1 预计算

这里我们需要构建两个LUT，分别为：

  • 变换矩阵$M$，其输入参数为各向同性BRDF的粗糙度与观察方向$\omega_o$
  • Fresnel矫正项，也就是预计算不同$\theta_o$和粗糙度下的 Fresnel 加权系数，存储为另一张 2D 纹理，从而补偿因线性变换忽略的 Fresnel 项
2.6.2 运行时
  1. 根据当前片段的粗糙度与$\theta_o=arccos(N\cdot\omega_o)$，从LUT中插值获取$M$与Fresnel项
  2. 获取面光源的几何参数（如矩形光的四个角点世界坐标），计算每个光源角点的规范空间坐标
  3. 裁剪光源到半球，从而提出规范空间中位于半球外的光源部分
  4. 计算规范空间中的余弦积分

2.7 零散的问题

由于我的水平实在有限，很多内容并没有在博客中详细讨论，所以这个小节用于整理这些内容，希望对LTC的理解有所帮助。

（1) 为什么需要补偿Fresnel项

Fresnel 项随入射角非线性变化，无法通过线性变换 M 直接嵌入规范空间。若直接将 Fresnel 项纳入变换矩阵 M，会破坏余弦分布的假设，导致积分无法解析求解。

(2) 什么是规范空间

规范空间是通过 线性变换矩阵 *M* 将实际空间（即真实世界中的 3D 空间）的几何和材质属性映射到的一个 标准化虚拟空间。

Unity, Rendering
Unity
本文由作者按照 CC BY 4.0 进行授权