The Rasterization Stage
Rasterization: What Are We Trying to Solve?
经过投影阶段,我们获取了三角形的顶点在二维栅格空间中的XY坐标,同时我们还保留了相机空间中顶点原始的Z坐标(包括取反以获取一个正数)
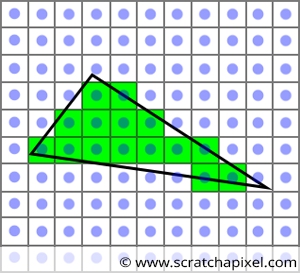
我们下一步需要做的是遍历图像中的像素,通过测试是否像素会与当前三角形的投影图形重叠,我们可以绘制出该三角形的图像,这也是光栅化的原理。如下图所示:
在图形API中,我们将这一步称为inside-outside test或converage test。在本篇博客中,我们将介绍实现覆盖测试的方法,即edge function。同时,我们还会引出重心坐标这个概念,它不仅能表示像素在三角形投影图像中的位置,还在计算真正的Z值中起着重要作用。
Edge Function
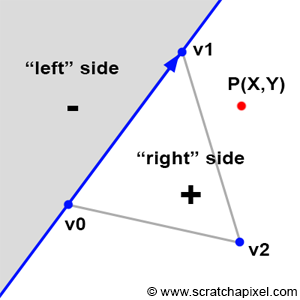
首先,我们可以将三角形的一条边视为一条直线,这条直线将三角形所在的平面分为了两部分,如下图所示。edge function的作用是,给定一个点,如果该点在这条线的右侧,则函数返回一个正数,否则就返回一个负数。如果给定点位于线上,则返回0。
如图中所示,如果我们为三角形的每条边都执行edge function,我们能够得到这样的结论:只有三角形内部的点才能满足三个edge function都返回正数。我们拓展一下,如果给定的点是一个像素的中心点,那我们就能够判断当前像素是否在三角形内部。
我们现在理解了edge function的原理,现在我们给出edge function的定义如下:
\[E_{01}(P) = (P.x - V0.x) \times (V1.y - V0.y) - (P.y - V0.y) \times (V1.x - V0.x).\]我们可以发现,edge function在数学上等价于由向量$(P-V0)$和向量$(V1-V0)$构成的2x2矩阵的的行列式,或者说是向量$(P-V0)$和向量$(V1-V0)$的叉积。不管是行列式还是叉积,它们的几何意义都是向量$(P-V0)$和向量$(V1-V0)$所构成的平行四边形的面积。
我们可以通过代码表示使用edge function判断给定点是否在三角形内部的过程:
1
2
3
4
5
6
7
8
9
10
11
12
13
bool edgeFunction(const Vec2f &a, const Vec3f &b, const Vec2f &c) {
return ((c.x - a.x) * (b.y - a.y) - (c.y - a.y) * (b.x - a.x) >= 0);
}
bool inside = true;
inside &= edgeFunction(V0, V1, p);
inside &= edgeFunction(V1, V2, p);
inside &= edgeFunction(V2, V0, p);
if (inside) {
// point p is inside the triangle defined by vertices V0, V1, V2
...
}
Winding Order Matters
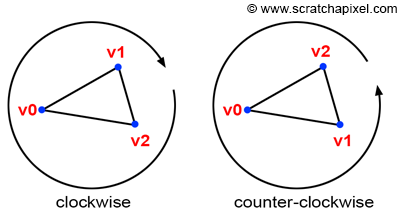
在edge function中,我们忽略了计算机图形学中一个相当重要的概念,也就是组成三角形的顶点的声明顺序,又称环绕方式winding。winding有两种方式,如下图所示,分别是顺时针CW以及逆时针CCW。
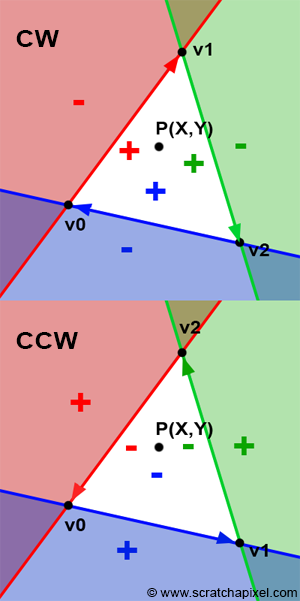
环绕方式如此重要,是因为它定义了三角形的一个重要属性:法线的朝向。回想一下,三角形的法线可以通过两个向量叉积计算得到,但我们也知道,叉积运算不满足交换率,那么在不同的环绕方式下,用于叉积运算的向量则分别会是$A\times B$与$B \times A$,自然会得到一组方向相反的法线。法线的方向在渲染中很重要,不仅与着色相关,还涉及到剔除的问题,也就是我们不会渲染那些背向相机的三角形。
我们回到edge function上,因为edge function本质上就是叉积运算,就自然会受到顶点顺序的影响。
本系列博客采用CW作为环绕方向。
Barycentric Coordinates
我们前面提到过,如果edge function的计算结果为正,我们就可以将其视为一个平行四边形的面积,可以直接用于计算当前像素的重心坐标。只是在我们深入了解之前,我们最好先回顾一下重心坐标的概念。
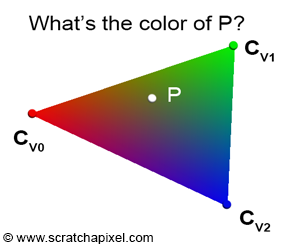
重心坐标由三个浮点数组成,我们表示为$\lambda_0$、$\lambda_1$、$\lambda_2$。重心坐标的意义在于,我们可以通过重心坐标和三角形的三个顶点,通过下面这个式子,来定义三角形上的任意一点的位置:
\[P = \lambda_0 \cdot V0 + \lambda_1 \cdot V1 + \lambda_2 \cdot V2.\]其中$\lambda_0$、$\lambda_1$、$\lambda_2$可以在任意范围中取值,但如果要表示三角形内中一点,则需要重心坐标需要同时满足两个条件:
- $\lambda_0$、$\lambda_1$、$\lambda_2$的取值范围均为$[0, 1]$
- $\lambda_0 + \lambda_1 + \lambda_2 = 1$
在数学上,这是线性插值的形式, 所以,我们还可以将重心坐标理解为三角形三个顶点对于三角形内一点的权重。如果已知三角形顶点坐标和给定点的重心坐标,我们可以通过线性插值计算出给定点的坐标。只是,在光栅化算法中,给定点的坐标我们是通过空间变换计算的。但基于同样的思路,我们可以通过重心坐标,在三角形表面上,插值计算三角形顶点的其他属性。
例如,我们为三角形的三个顶点各赋予一个颜色值,如下图所示。如果我们计算得到了点P的重心坐标,我们就可以通过线性插值的方式计算出点P的颜色值,即$C_P = \lambda_0 \cdot C_{V0} + \lambda_1 \cdot C_{V1} + \lambda_2 \cdot C_{V2}$
除了颜色值,常见的顶点属性还包括纹理坐标、法线等。
现在我们的问题是,如果计算重心坐标呢?我们就忽略推导的过程了,直接给出结论与步骤。
根据重心坐标的定义,点P在三角形ABC内的位置可以由三角形面积的比例来表示,由于是比例运算,就等同于平行四边形的面积比例,而平行四边形的面积刚好是edge function的计算结果。这样的话,计算重心坐标的过程就大大得到了简化。
对应的代码实现如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
float edgeFunction(const Vec3f &a, const Vec3f &b, const Vec3f &c)
{
return (c.x - a.x) * (b.y - a.y) - (c.y - a.y) * (b.x - a.x);
}
float area = edgeFunction(v0, v1, v2); // Area of the triangle multiplied by 2
float w0 = edgeFunction(v1, v2, p); // Signed area of the triangle v1v2p multiplied by 2
float w1 = edgeFunction(v2, v0, p); // Signed area of the triangle v2v0p multiplied by 2
float w2 = edgeFunction(v0, v1, p); // Signed area of the triangle v0v1p multiplied by 2
// If point p is inside triangles defined by vertices v0, v1, v2
if (w0 >= 0 && w1 >= 0 && w2 >= 0) {
// Barycentric coordinates are the areas of the sub-triangles divided by the area of the main triangle
w0 /= area;
w1 /= area;
w2 /= area;
}
在这里,我们提前讨论一个简单易行的优化手段。首先我们知道通过下面的式子,我们可以计算出三角形表面的任意值:
\[Z = \lambda_0 \cdot Z0 + \lambda_1 \cdot Z1 + \lambda_2 \cdot Z2.\]我们将$\lambda_0 + \lambda_1 + \lambda_2 = 1$代入其中,可得:
\[Z = Z0 + \lambda_1(Z1 - Z0) + \lambda_2(Z2 - Z0).\]其中,$Z1 - Z0$和$Z2 - Z0$都是可以预先计算的常量,因此,我们就将$Z$的计算简化到了两次乘法加两次加法。
Rasterization Rules
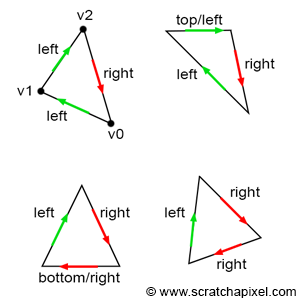
某些情况下,一个像素可能与多个三角形重叠,特别是当像素位于两个三角形的公共边上时,此时,该像素在两个三角形的coverage test中都可以通过。对于这种情况,我们需要确定某种规则,用于确保像素不会与共享一条边的两个三角形重叠两次。大多数的图形API都定义了所谓的top-left rule。该规则规定,如果像素位于三角形内部,或位于三角形的顶边或左边的边上时,则视该像素与三角形重叠。下图中,我们可以看到所谓的顶边和左边的边的示意:
- top edge:水平的边,并且组成该边的两点在第三个点上方。
- left edge:上升的边,即两点的Y坐标是升序的。
需要注意的是,左边和顶边的定义受环绕方式的影响。
我们的光栅化程序暂时不会使用这个规则。