文章

The Projection Stage

发表于
作者 褴褛飞旋
9 分钟阅读

Quick Review

我们可以将光栅化算法分为两个部分：

  • Project Stage：将三角形顶点投影到canvas上
  • Rasterization Stage：光栅化三角形，也就是将三角形拆分为像素的过程。

我们将各用一篇博客来深入两个部分，本篇博客先探讨Projection Stage。

在本篇博客中的主要内容如下：

  • 回顾顶点的变换过程
  • 探讨投影相关的新技术，这些新技术在构建透视投影矩阵中很重要
  • 介绍将屏幕空间的投影点重映射到NDC空间的新方法
  • 探讨Z坐标在光栅化算法中的作用，以及在投影阶段的处理

Projection：What Are We Trying to Solve?

光栅化的原理是判断图像中的像素是否与三角形重叠。为了实现这一点，我们首先需要将三角形投影到canvas上，然后将三角形的顶点从屏幕空间映射到NDC空间，再映射到栅格空间，从而让三角形和像素定义在同一个空间中，从而能够判断重叠。

所以，投影阶段的任务就是将构成三角形的顶点从相机空间变换到栅格空间，从而得到像素的坐标

Projecting Vertices: Mind the Z-Coordinates

此前，当我们计算三维顶点在栅格空间中的坐标时，我们最终想得到的是X坐标和Y坐标，也就是顶点在图像中的位置。回想一下，我们首先会对相机空间中的点进行透视除法，获得一个二维的点，同时由于投影点位于近裁截面上，我们还需要乘以近裁截面与相机之间的距离，即：

\[\begin{array}{l} P_{\text{screen}}.x = \dfrac{ \text{near} \times P_{\text{camera}}.x }{ -P_{\text{camera}}.z }\\ P_{\text{screen}}.y = \dfrac{ \text{near} \times P_{\text{camera}}.y }{ -P_{\text{camera}}.z }\\ \end{array}\]

但是，我们一直忽略了Z坐标，也就是在透视除法完成后就丢弃了Z坐标相关的数据。但是现在，我们会将屏幕空间中的点声明为一个三维的点，需要注意的是，由于相机空间中的Z坐标都是负数，我们需要取反，使得屏幕空间中的顶点的Z坐标为正数，即：

\[\begin{array}{l} P_{\text{screen}}.x = \dfrac{ \text{near} \times P_{\text{camera}}.x }{ -P_{\text{camera}}.z }\\ P_{\text{screen}}.y = \dfrac{ \text{near} \times P_{\text{camera}}.y }{ -P_{\text{camera}}.z }\\ P_{\text{screen}}.z = { -P_{\text{camera}}.z }\\ \end{array}\]

将屏幕空间上的顶点声明为一个三维顶点，而非二维，这也意味着屏幕空间实际上是一个三维空间。

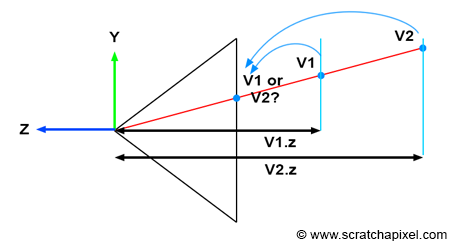
为什么我们需要保留相机空间中的Z值呢？试想，在场景中，如果两个顶点经过投影阶段处理后，具有相同的栅格坐标，那我们要如何决定哪个顶点是可见的呢？此时，如果我们比较两个顶点在栅格空间中的Z值，那么就有较小Z值的顶点一定距离相机更近，也就是可见的，而距离较远的顶点是不可见的。下图演示了Z值的重要作用

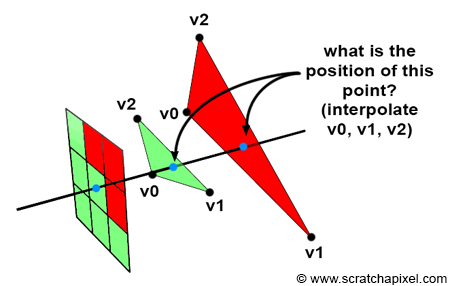
当我们要渲染三角形而非单个顶点时，Z值起着类似的作用。从下图可以看到，在栅格阶段，如果一个像素与多个三角形重叠，那么通过判断像素的Z值，我们就可以知道哪个三角形距离相机更近。当然，当前我们对于栅格阶段的了解还不够深入，后面我们会展开探讨。

只是，虽然概念上我们将屏幕空间中的投影点声明为三维顶点，但实际上，我们直到栅格阶段才会使用屏幕空间中投影点的Z值，那么我们不妨仍然将其声明为二维点，但会将栅格坐标声明为三维点，并将其Z值设定为$-pCamera.z$。

Remapping Screen Space Coordinates to NDC Space

之前，我们说屏幕空间中的坐标需要再次映射到NDC空间中，同时，在NDC空间中，canvas上的投影点的坐标值都在$[0, 1]$的范围上。但实际上，GPU中的NDC空间的坐标范围是$[-1, 1]$，虽然两种范围都是可行的，但我们最好还是按照GPU的光栅化标准进行处理。

我们分别用$l, r, b, t$来表示canvas的左、右、下、上的范围，也就是说，当屏幕空间的可见的投影点的范围分别是$[l, r]$和$[b, t]$。这样的话，我们就可以推导出将坐标映射到NDC空间中式子了，我们这里省略推导过程，直接给出结果：

\[\displaylines{-1 < \color{red}{\frac{2x}{r - l}} \color{green}{- \frac{r + l}{r-l}} < 1 \\ -1 < \color{red}{\frac{2y}{t - b}} \color{green}{- \frac{t + b}{t-b}} < 1}\]

这两个式子相当重要，因为红色和绿色标记的项，就会变成透视投影矩阵的系数，我们会在后面解释。现在，我们可以通过这两个式子将屏幕空间中的点的XY坐标映射到$[-1, 1]$的范围中，也就是映射到NDC空间。

Putting Together

我们对于之前的投影阶段进行一些改进，包括：

  • 为栅格空间中的像素坐标保留相机空间中的Z值
  • 将NDC空间的XY坐标范围修改为$[-1, 1]$，而不是此前的$[0, 1]$。

当我们将坐标从NDC空间映射到栅格空间时，我们只需要将坐标先映射到$[0, 1]$，然后将坐标分别乘以图片宽度和高度，(需要留意对Y坐标的处理，因为NDC空间与栅格空间中，Y轴的方向刚好相反）

我们用代码表示出整个投影阶段的过程，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

float nearClippingPlane = 0.1f;
Point3f pCamera;
worldToCamera.multiVecMatrix(pWorld, pCamera);
// convert to screen space
Point2f pScreen;
pScreen.x = nearClippingPlane * pCamera.x / -pCamera.z;
pScreen.y = nearClippingPlane * pCamera.y / -pCamera.z;
// convert to NDC space (range [-1, 1])
Point2f pNDC;
pNDC.x = 2 * pScreen.x / (r - l) - (r + l) / (r - l);
pNDC.y = 2 * pScreen.y / (t - b) - (t + b) / (t - b);
// convert to raster space, and set pRaster.z as -pCamera.z
Point3f pRaster;
pRaster.x = (pNDC.x + 1) / 2 * imageWidth;
pRaster.y = (1 - pNDC.y) / 2 * imageHeight; // In raster space, y-direction is inverted
pRaster.z = -pCamera.z;

需要注意的是，由于现在我们将Z坐标存储在栅格空间中，我们将栅格坐标，也就是像素坐标，声明为浮点数值，而非此前的整数值。

Graphics, Build A Soft Rasterizer
本文由作者按照 CC BY 4.0 进行授权