Ch08 Light and Color
Radiometry 辐射度学
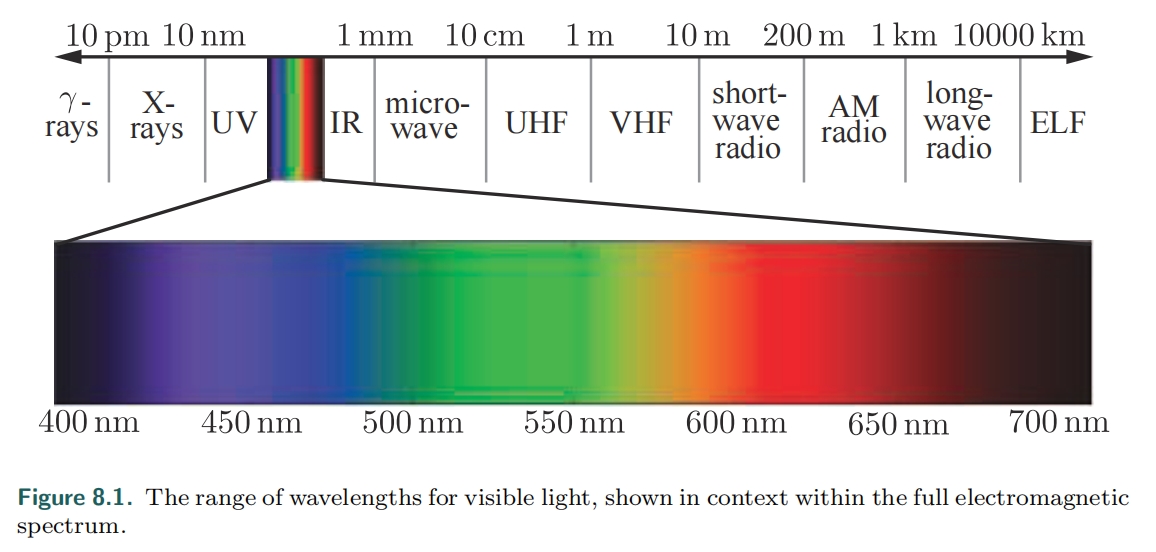
不同波长的电磁波具有不同的属性。人类肉眼可见的电磁波的波长范围为400纳米到700纳米。如下图所示:
在基于物理的渲染中,我们围绕以下四个辐射度量学中的物理量展开:
| Name | Symbol | Units |
|---|---|---|
| radiant flux | $\Phi$ | $W$ |
| irradiance | $E$ | $W/m^2$ |
| radiant intensity | $I$ | $W/sr$ |
| radiance | $L$ | $W/(m^2sr)$ |
在辐射度量学中,最基本的单位为radiant flux,记为$\Phi$,这是一个表示单位时间内通过的辐射量的物理量,我们可以将其理解为一个表示“功率”的概念,单位为$W$。
Irradiance则表示单位面积上radiant flux的密度,记为$E(d\Phi /dA)$,单位为$W/m^2$。irradiance是一个关于面积的物理量,在渲染领域中,我们可以将面积理解为物体的“表面”。
在介绍下一个物理量之间,我们需要先引入立体角这个概念。它是三维空间中度量一个面从球心所张开的空间角度的量,记为$\omega$, 单位为steradian球面度,简写为$sr$。立体角的大小与球面投影面积直接相关,其定义式为:$\omega = A /r^2$。
建立在立体角的基础上,radiance intensity,表示单位立体角上的radiance flux,记为$I(d\Phi / d\omega)$,单位为$W/sr$。
最终,我们可以引入用于表示单个射线上辐射量的物理量,radiance。更确切地来说,它定义为单位面积、单位立体角上的radiant flux的密度,记为$L(d^2\Phi/dAd\omega)$。需要注意的是,radiance所定义的射线与其所在的面积是相互垂直的。所以,如果将radiance应用于其他角度的观察方向上时,我们需要额外引入一个余弦矫正参数。radiance作为人眼、相机等传感系统所测量的值,是渲染领域中最重要的物理量。我们计算渲染方程的目的,就是得到从给定着色点到相机所在射线上的radiance。此外,radiance具有一个重要的性质,那就是其值不受距离的影响。
通常来说,光线会包含多种不同波长的光波。我们用光谱功率分布(Spectral Power Distribution, SPD)来描述光源在不同波长上辐射功率的分布情况。在渲染领域中,我们不会使用到完整的SPD,而是以RGB三元组的形式来表示各个辐射度量学中的物理量。我们会在后文中介绍该三元组如何与光谱分布相对应。
Photometry 光度学
辐射度学与光度学都是描述光能量的学科,但光度学更多地考量了人眼的视觉响应,即对于不同波长的感知敏感度。此外,辐射度学使用的是绝对物理单位,如$W$,而光度学则使用例如流明这样的单位。具体的单位对应关系如下:
| Radiometric Quantity: Units | Photometric Quantity: Units |
|---|---|
| radiant flux: $W$ | luminous flux: lumen ($lm$) |
| irradiance: $W/m^2$ | illuminance: lux ($lx$) |
| radiant intensity: $W/sr$ | luminous intensity: candela ($cd$) |
| radiance: $W/m^2sr$ | luminance: $cd/m^2=nit$ |
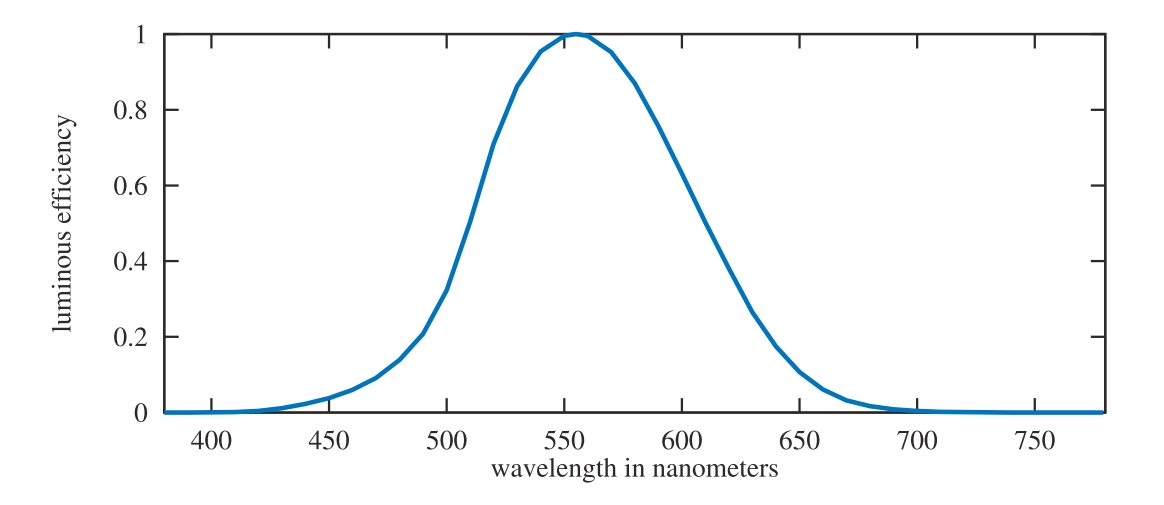
我们通过CIE photometric curve来将辐射度学的计算结果转换到光度学中的单位值,这是一个以555纳米为中心的钟形曲线,表示了人眼对于不同波长的响应,如下图所示:
Colorimetry 色度学
色度学的研究基于以下几个关键要素:
- 光谱分布:光的颜色由其光谱功率分布(Spectral Power Distribution, SPD)决定。
- 人眼感知:颜色感知依赖于人眼的三种视锥细胞(对红、绿、蓝敏感)对不同波长光的响应
- 颜色空间:颜色用数学方式表示,常见的颜色空间包括 CIE 1931 XYZ 和 RGB。
色度学定义了一个色品匹配函数,可以将光谱数据转换为颜色表示,具体来说,是通过XYZ三个坐标值来定义一个颜色的色品与亮度。