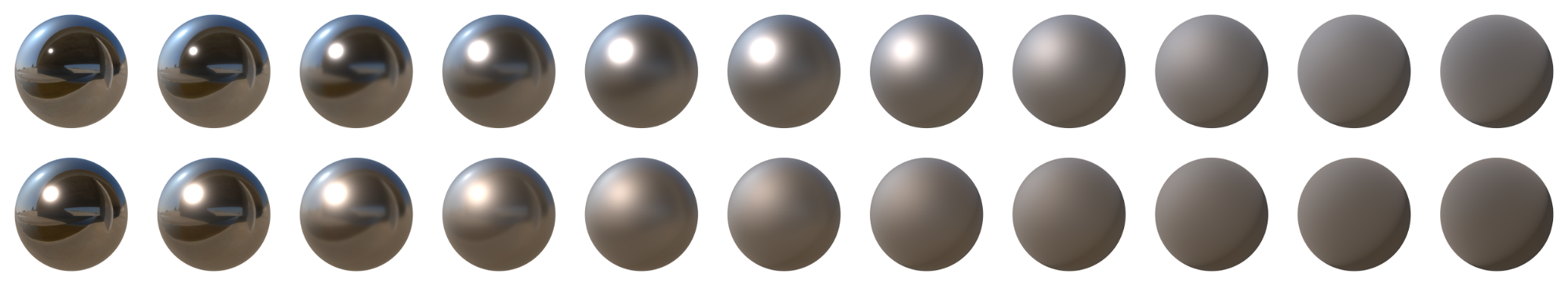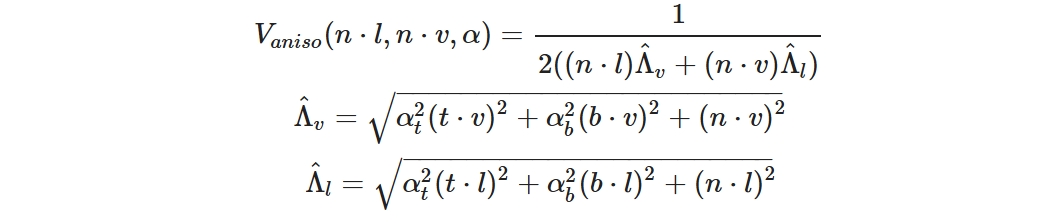Material System in Filament

1 Standard model

我们材质模型的目标是描述标准材质外观。从数学上，材质模型通过BSDF（双向散射分布函数）表述，该函数由BRDF（双向反射分布函数）与BTDF（双向透射分布函数）共同构成。

由于聚焦常见表面类型，标准材质模型将重点处理BRDF，对BTDF进行忽略或高度简化。因此，该标准模型仅能准确模拟具有短平均自由程的反射型、各向同性、介电或导电材质表面。其中，短平均自由程表示光线在材质内部的散射距离小于像素尺度。

BRDF将标准材质的表面响应表述为两个项的函数：

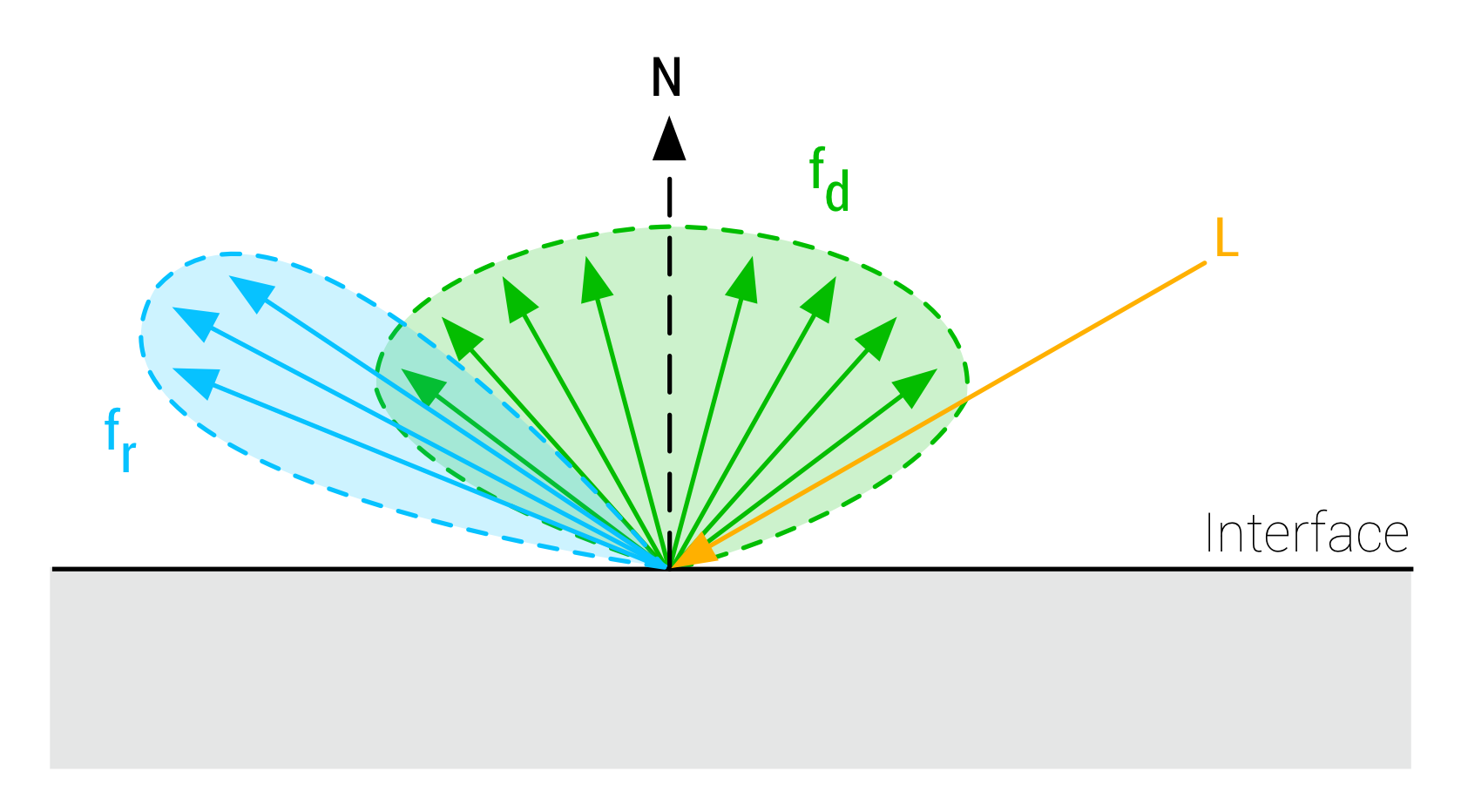
• 漫反射部分，记为$f_d$
• 镜面反射部分，记为$f_r$

下图展示了表面、表面法线、入射光线与上述两个项之间的关系（暂时忽略次表面散射）：

BRDF的数学表达式为：

\[\begin{equation}\label{brdf} f(v,l)=f_d(v,l)+f_r(v,l) \end{equation}\]

该方程描述了单一入射光方向的表面响应。完整的渲染方程需要在半球空间对所有入射光方向进行积分计算。

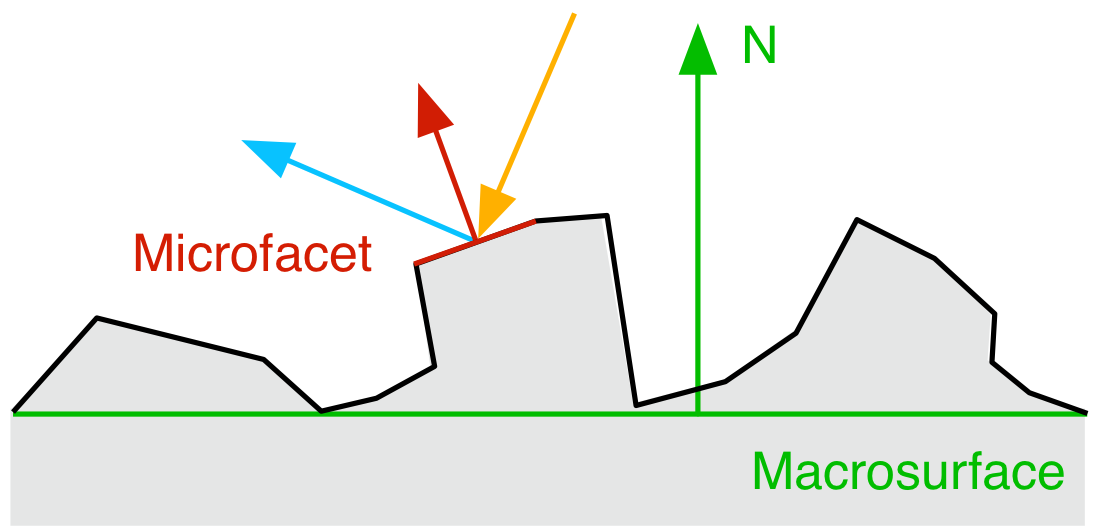
常见材质表面并非完全平坦，因此需要能描述光线与不规则界面交互的模型。微表面BRDF为此提供了物理可信的解决方案，该理论认为微观层面表面由大量随机排列的平面片段（即微表面）构成。下图展示了微观尺度下平坦界面与不规则界面的差异。

我们从下图中可以看出，只有当微表面的法线方向指向半程向量时，才能被观察到：

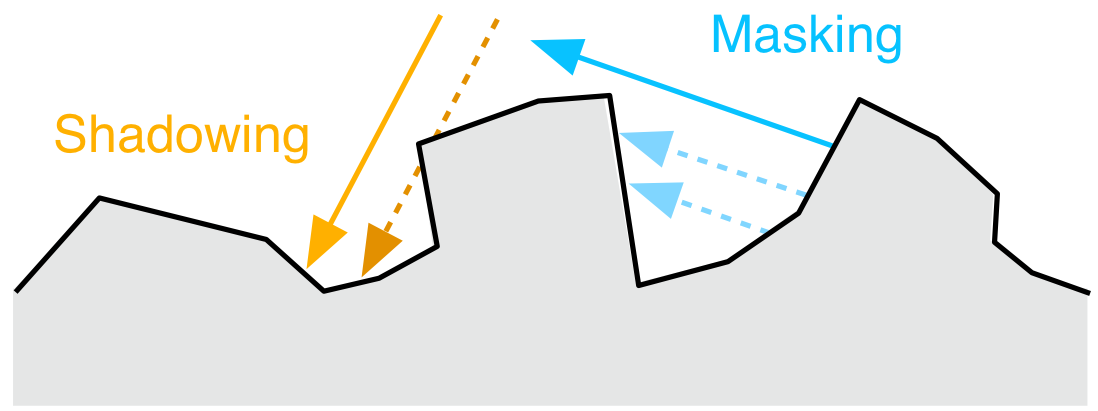
但是这并非是微表面可见的充分条件，在BRDF中，我们同样需要考虑到遮蔽masking与阴影shadowing，如下图所示：

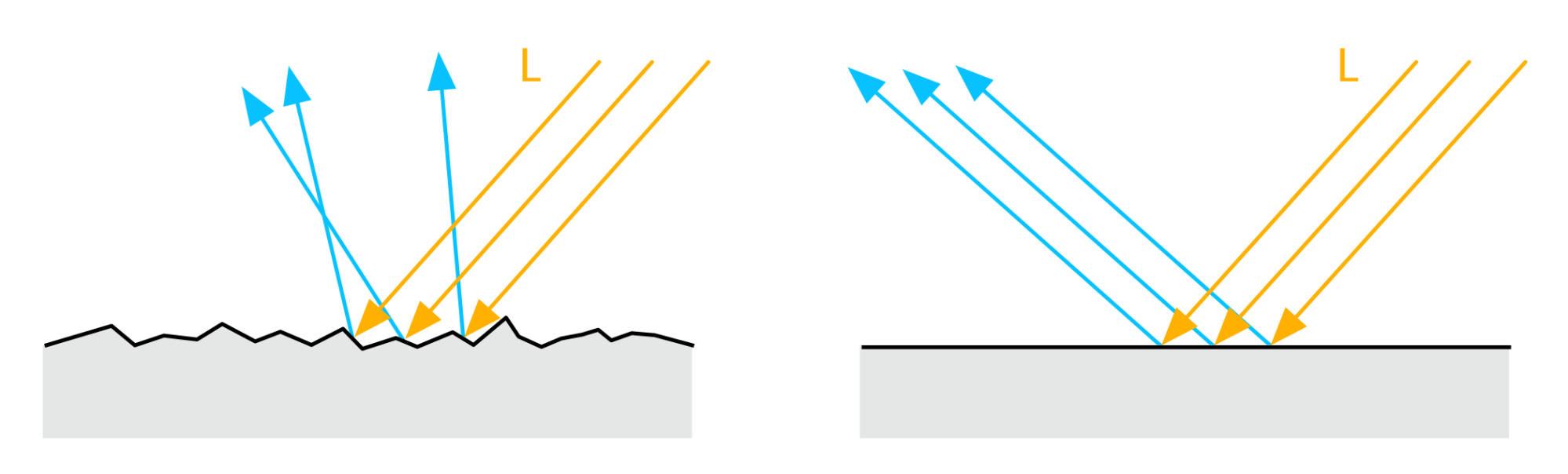
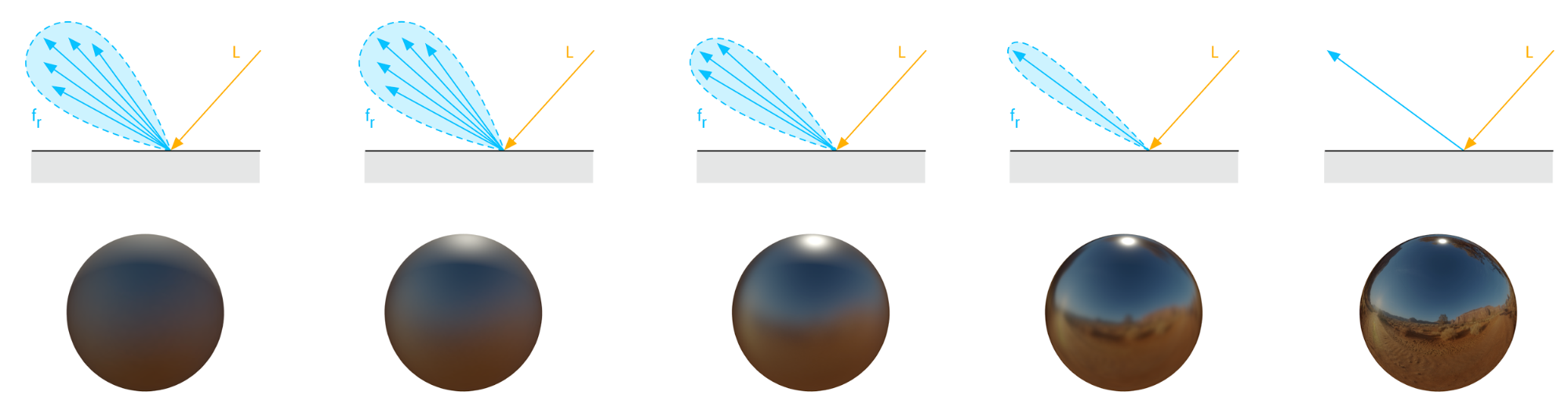
微表面BRDF的核心受粗糙度参数支配，该参数描述微观层面的表面光滑度或粗糙度。表面越光滑，微面排列越有序，反射光越集中；表面越粗糙，朝向视线的微面越少，反射光线散射偏离视线方向，导致镜面高光模糊化。下图展示了不同粗糙度的表面与光线之间的交互：

在本篇博客所展示的GLSL代码中，用户设置的粗糙度参数称为perceptualRoughness（感知粗糙度），实际使用的roughness变量是经过重映射处理的版本，我们会在后面的章节中涉及到这一方面

微表面模型可以通过下面的数学表达式进行描述：

\[f_x(v, l)=\frac{1}{|n\cdot v||n \cdot l|}\int_{\Omega}D(m, \alpha)G(v,l,m)f_m(v, l, m)(v\cdot m)(l\cdot m)dm\]

其中：

• $x$代表镜面或漫反射部分
• $D$项用于建模微表面的分布，又可以称为法线分布函数NDF
• $G$项用于建模微表面的可见性，或者称之为geometry occlusion或shadow-masking

我们上述这个渲染方程对于漫反射部分或镜面反射部分都成立，所以区别就在于BRDF，即$f_m(v, l, m)$的实现上。

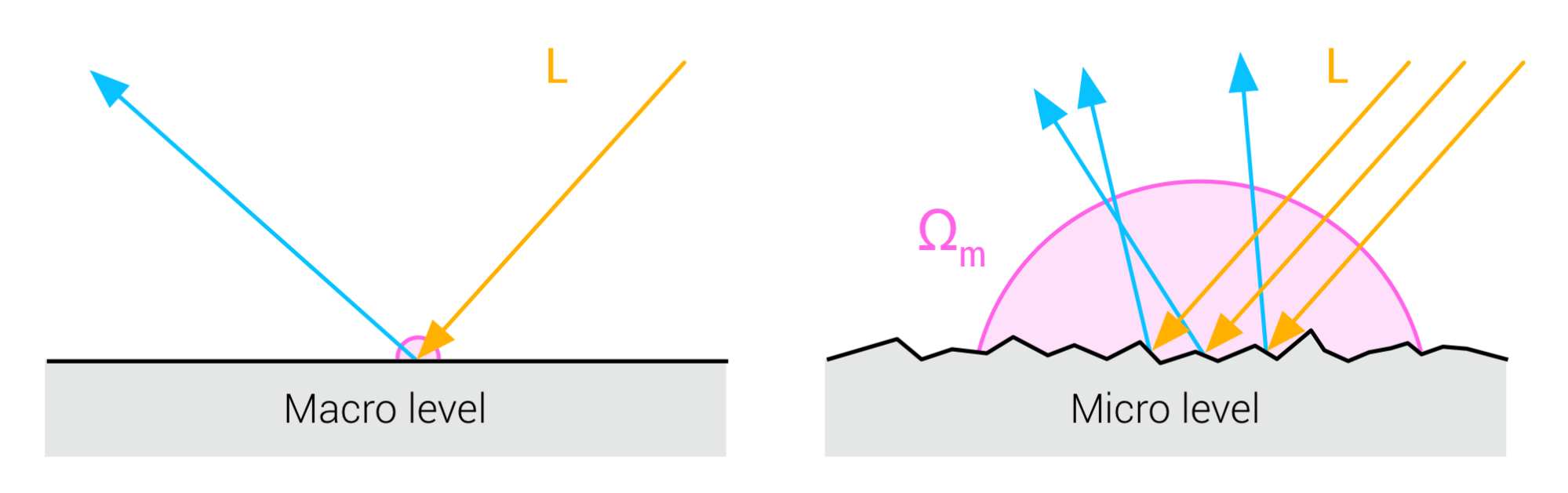
需要注意的是，此方程用于在微观层面上对半球进行积分，如下图所示：

上图显示，在宏观层面将表面视为平整的面的这种简化假设允许将单个光照方向的着色片段对应到表面上单一一点，从而简化渲染方程。

而在微观层面上，表面是不平坦的，我们也不能再认为只有一条单一的光线，而是应该假设存在一束方向平行的光线。在微表面理论中，这束光线会被散射到各个方向上，由此我们必须在半球上对表面的交互进行积分，也就是图中所标注的$\Omega_m$。

但是为每个片段都进行半球上的积分显然是不可行的，所以不管是漫反射还是镜面反射，我们都需要使用积分的近似。

---

2 Dielectrics and conductors

在深入BRDF的实现之前，我们还需要了解一下金属与非金属之间的区别。

前文提到，当入射光线作用于由BRDF控制的表面时，光线会被分解为两个独立的反射分量：漫反射（diffuse reflectance）与镜面反射（specular reflectance）。这一行为的模型化过程直观明了，如下图所示：

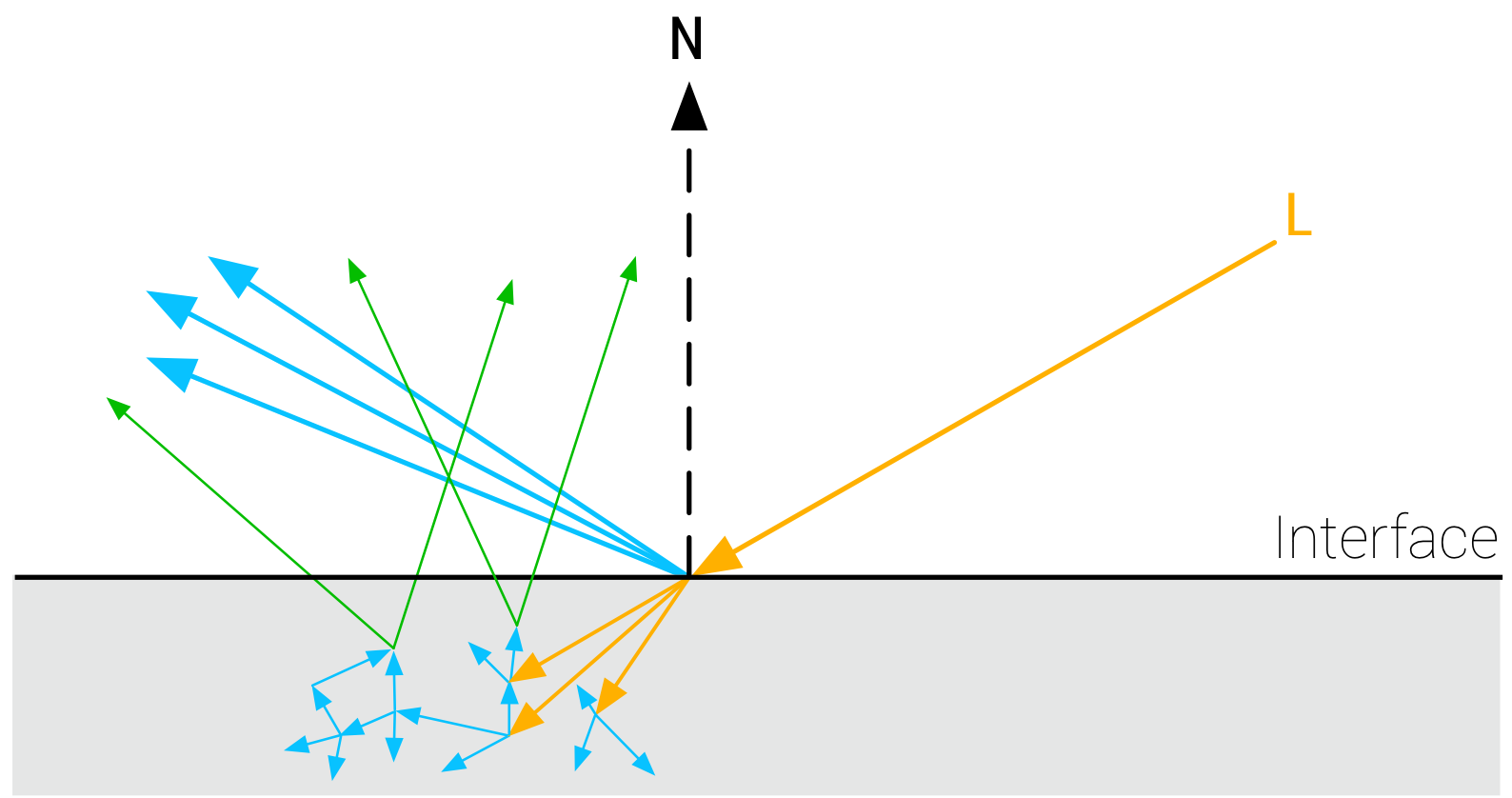
这种建模方法是对光线与表面真实作用方式的简化。实际上，部分入射光会穿透表面，在内部发生散射，并再次穿出表面形成漫反射，如下图所示：

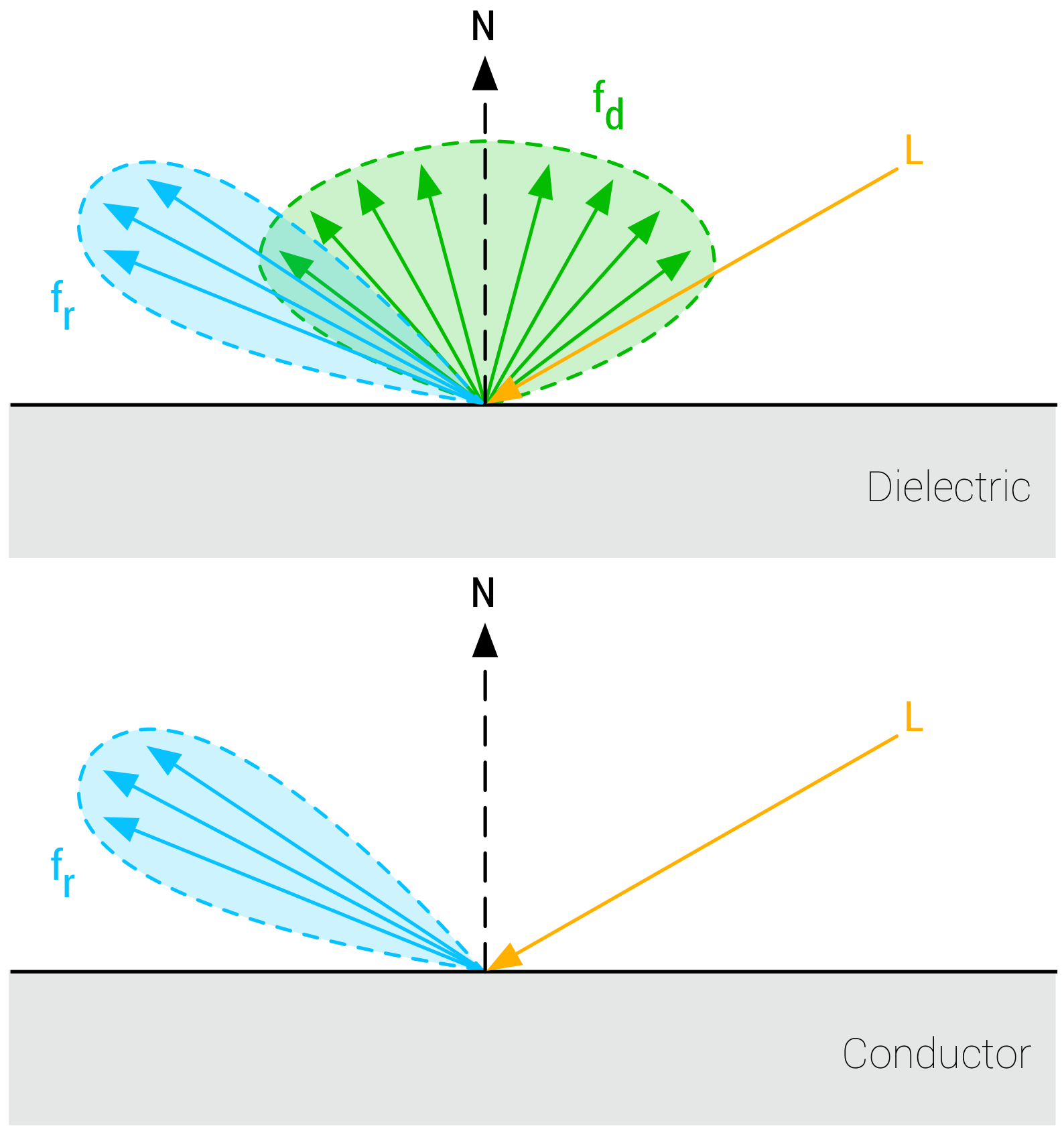
这就是金属与非金属材质的区别所在，纯金属材质不会发生次表面反射，也就是说在BRDF模型中，没有漫反射的部分。而散射会发生在非金属材质上，也就是说，非金属材质同时有漫反射与镜面反射。二者之间的区别如下图所示：

---

3 Energy conservation

在PBR渲染中，能量守恒是一个关键的概念。在能量守恒的BRDF模型中，镜面反射与漫反射的能量之和要小于入射能量的总和。

---

4 Specular BRDF

对于镜面反射的部分$f_r$，其本质是一个遵循菲涅尔定律的mirror BRDF，在微表面模型积分（Cook-Torrance近似）中，该定律以$F$表示：

\[f_r(v, l)=\frac{D(h,\alpha)G(v, l, \alpha)F(v, h, f0)}{4(n\cdot v)(n \cdot l)}\]

出于实时渲染的限制，我们必须使用$D$、 $G$、$F$这三项的近似计算方式。我们将在下面的小节中讨论具体的近似方式。

4.1 D: Normal distribution function

GGX模型使用了一种更接近现实的微表面法线分布函数NDF，能够模拟具有粗糙表面的物体。其分布函数具有较长的尾部（”heavy tail”），这使得它能够更好地表现表面粗糙度较低但仍有高光区域的物体。公式如下：

\[D_{GGX}(h,\alpha)=\frac{\alpha^2}{\pi((n\cdot h)^2(\alpha^2-1)+1)^2}\]

4.2 G: Geometric shadowing

首先，我们给出模拟几何阴影的Smith公式：

\[G(v,l,\alpha)=G_1(l,\alpha)G_1(v,\alpha)\]

其中，$G_1$由多个可选的模型，我们通常会使用GGX公式（以$v$为例）：

\[G_1(v,\alpha)=G_{GGX}(v,\alpha)=\frac{2(n\cdot v)}{n\cdot v + \sqrt{\alpha^2+(1-\alpha^2)(n\cdot v)^2}}\]

这样的话，我们就可以给出完整的Smith-GGX公式：

\[G(v,l,\alpha)=\frac{2(n\cdot l)}{n\cdot l + \sqrt{\alpha^2+(1-\alpha^2)(n\cdot l)^2}} \frac{2(n\cdot v)}{n\cdot v + \sqrt{\alpha^2+(1-\alpha^2)(n\cdot v)^2}}\]

我们可以注意到，此公式的分子刚好可以与BRDF公式中的分母约去，所以我们不妨在BRDF引入一个新的可视性函数$V$：

\[f_r(v,l)=D(h,\alpha)V(v, l, \alpha)F(v, h, f_0)\]

其中：

\[V(v, l, \alpha)=\frac{G(v,l,\alpha)}{4(n\cdot v)(n \cdot l)}=V_1(l, \alpha)V_1(v, \alpha)\]

此外，Heitz提出，将微表面的高度纳入到计算中，以矫正masking和shadowing，从而能够带来更精准的结果。高度矫正的Smith公式如下：

\[G(v,l,h,\alpha)=\frac{\chi^+(v \cdot h)\chi^+(l \cdot h)}{1+\Lambda(v)+\Lambda(l)}\]

其中，$\Lambda$为：

\[\Lambda(v)=\frac{1}{2}\Big( \frac{\sqrt{\alpha^2+(1-\alpha^2)(n\cdot v)^2}}{n\cdot v} -1 \Big)\]

可得：

\[V(l, v, a)= \frac{0.5}{(n\cdot v)\sqrt{a^2+(1-a^2)(n\cdot l)^2}+(n\cdot l)\sqrt{a^2+(1-a^2)(n\cdot v)^2}}\]

我们观察可以发现，平方根中的项都是平方数，并且所有的项的范围都为$[0, 1]$，所以我们可以利用近似来获得一个优化的可视性函数：

\(V(v,l,\alpha=\frac{0.5}{n\cdot l(n\cdot v(1-\alpha)+\alpha)+n\cdot v(n\cdot l(1-\alpha)+\alpha)}\) Hammon所使用的近似方案为：

\[V(v,l,\alpha=\frac{0.5}{lerp(2(n\cdot l)(n\cdot v), n\cdot l + n\cdot v, \alpha)}\]

4.3 Specular F

菲涅尔效应在基于物理的材质外观表现中起着关键作用。该效应揭示了观察者所见表面反射光的强度取决于视角角度。大面积水域是体验此现象的绝佳范例，如下图所示。当垂直俯视水面（法线入射角）时，水体呈现透明状态；而随着视线逐渐转向远处（掠射角，此时光线趋于与表面平行），水面镜面反射强度显著增强。

实际上，反射强度不仅取决于观察角度，同样会收到材质IOR的影响。我们将垂直入射时反射的光量记为$f_{0}$，将掠射时反射的光量记为$f_{90}$。

我们可以规范一下对菲涅尔效应的描述：菲涅尔项定义了在两个不同的介质的相接面上，光的反射与折射情况，或者说反射能量与透射能量之比。

在Cook-Torrance BRDF模型中，我们使用Schlick近似来描述菲涅尔项：

\[F_{Schlick}(v, h, f_0, f_{90})=f_0+(f_{90}-f_0)(1-v\cdot h)^5\]

常数$f_0$表示垂直入射时的镜面反射率，对于电介质是无色的，对于金属是有色的。具体的值取决于材质的IOR系数。

实际上，我们可以讲这个菲涅尔函数看作在入射镜面反射率与掠射角处的反射率，即$f_{90}$，之间进行插值。观察现实世界，无论材质是否是金属还是非金属的，在掠射角均表现为无色的镜面反射，故我们可以将$f_{90}$设为1，从而得到简化的菲涅尔函数的实现：

vec3 F_Schlick(float u, vec3 f0) 
{
    float f = pow(1.0 - u, 5.0);
    return f + f0 * (1.0 - f);
}

---

5 Diffuse BRDF

对于漫反射，我们使用简单的Lambertian BRDF，也就是假设在整个微表面半球上，有均匀的漫反射，其数学表达式为：

\[f_d(v, l)=\frac{\sigma}{\pi}\]

而在代码实现中，我们通常会将漫反射反射率$\sigma$在后续中的步骤中乘上，例如：

float Fd_Lambert()
{
	return 1.0 / PI;
}

vec3 Fd = diffuseColor * Fd_Lambert();

Lambertian BRDF的计算相当高效，并且在一定程度上足以实现真实的材质外观。

然而，在理想情况下，漫反射部分应该与镜面反射一致地将表面的粗糙度考虑在内。Disney与Oren-Nayar两个漫反射模型都将粗糙度考虑在内，并且能在掠射角产生一些逆向反射retro-reflection。

至于使用哪种漫反射模型，需要在画质提升与因此而来的额外的计算开销之间进行权衡，通常来说，Lambertian仍然是一个常见的选择。

Disney漫反射模型的数学表达式如下：

\[f_d(v, l)=\frac{\sigma}{\pi}F_{Schlick}(n, l, 1, f_{90})F_{Schlick}(n, v, 1, f_{90})\]

其中：

\[f_{90}=0.5 + 2\cdot \alpha cos^2(\theta_d)\]

需要注意的是，我们在这里所介绍的迪士尼模型并不遵守能量守恒定律，而更倾向于一种经验模型。

---

6 Standard model summary

镜面反射部分：使用Cook-Torrance镜面微表面模型，包含基于GGX的法线分布函数，基于Smith-GGX的高度矫正的可见性函数，以及基于Schlick的菲涅尔函数

漫反射部分：Lambertian模型

完整的代码实现如下：

float D_GGX(float NoH, float a) {
    float a2 = a * a;
    float f = (NoH * a2 - NoH) * NoH + 1.0;
    return a2 / (PI * f * f);
}

vec3 F_Schlick(float u, vec3 f0) {
    return f0 + (vec3(1.0) - f0) * pow(1.0 - u, 5.0);
}

float V_SmithGGXCorrelated(float NoV, float NoL, float a) {
    float a2 = a * a;
    float GGXL = NoV * sqrt((-NoL * a2 + NoL) * NoL + a2);
    float GGXV = NoL * sqrt((-NoV * a2 + NoV) * NoV + a2);
    return 0.5 / (GGXV + GGXL);
}

float Fd_Lambert() {
    return 1.0 / PI;
}

void BRDF(...) {
    vec3 h = normalize(v + l);

    float NoV = abs(dot(n, v)) + 1e-5;
    float NoL = clamp(dot(n, l), 0.0, 1.0);
    float NoH = clamp(dot(n, h), 0.0, 1.0);
    float LoH = clamp(dot(l, h), 0.0, 1.0);

    // perceptually linear roughness to roughness (see parameterization)
    float roughness = perceptualRoughness * perceptualRoughness;

    float D = D_GGX(NoH, roughness);
    vec3  F = F_Schlick(LoH, f0);
    float V = V_SmithGGXCorrelated(NoV, NoL, roughness);

    // specular BRDF
    vec3 Fr = (D * V) * F;

    // diffuse BRDF
    vec3 Fd = diffuseColor * Fd_Lambert();

    // apply lighting...
}

---

7 Improving the BRDFs

正如我们前面所提到的，一个好的BRDF模型应该满足能量守恒定律。然而，我们目前所构建BRDF仍然存在两点问题：

7.1 Energy Gain in Diffuse Reflectance

Lambert漫反射模型没有考虑到表面反射的光，换句话说，兰伯特模型假设光线在进入表面并且在表面内部反射散射后重新从表面反射出来，但是它忽略了表面上可能发生的反射。

实际的表面通常不会完全是漫反射的，很多材质在某些角度下会有明显的反射效果（比如玻璃或金属表面），这些反射的光并不会参与到漫反射事件中，而是直接被反射回去。所以说，Lambert模型并没有考虑这种反射现象，因此它的适用范围是非常简化的，通常用在模拟那些表现出理想漫反射性质的材质上。

7.2 Energy Loss in Specular Reflectance

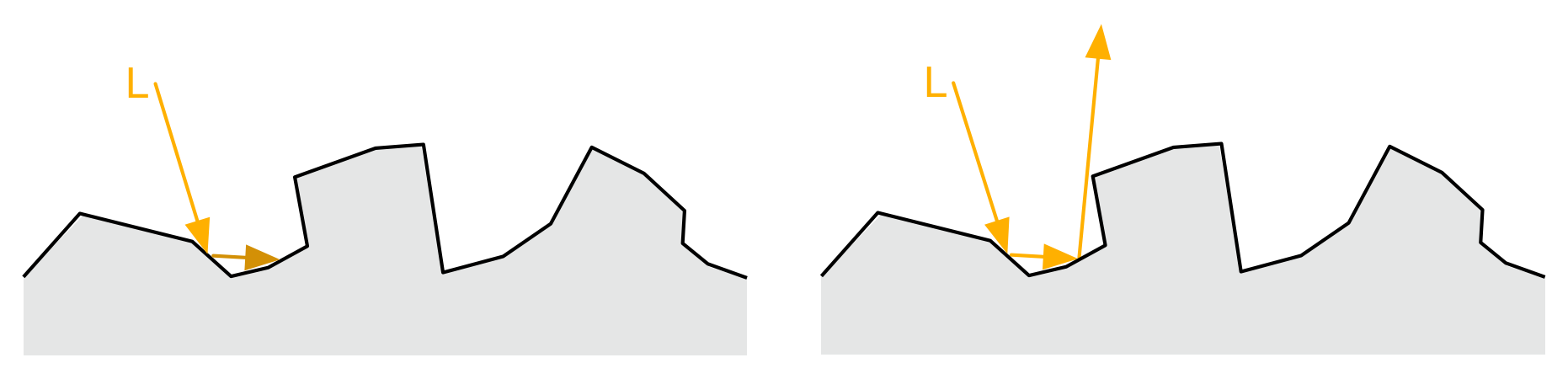
我们所讨论的Cook-Torrance BRDF试图在微观层面上对多个事件进行建模，但是它所成立的基础是仅仅考虑光线的单次反射。对于较高的粗糙度来说，Cook-Torrance BRDF会带来一些能量损失。如下图所示，如果只考虑光线的单次反射，那么图中的光线会由于shadowing与masking项而被丢弃，但如果考虑到光线的多次反射，也存在光线在多次反射后进入观察者视线中的可能：

基于这个简单的解释，我们可以得到这样的结论：表面越粗糙，则由于没考虑到多次散射而导致的能量损失的可能性就越大。这种能量损失最终将导致材质变暗，对于金属材质来说，这种现象尤为明显，因为金属材质所有的反射都是高光反射。

Kulla and Conty提出了一种基于IBL的能量补偿方案：增加一个能量补偿的项，作为一个额外的BRDF lobe。这部分内容我会在后续进行补充。

---

8 Parameterization

Parameter	Definition
BaseColor	非金属表面：漫反射albedo；金属表面：specular color
Metallic	界定一个表面是金属还是非金属
Roughness	表面的感知粗糙程度。光滑的表面呈现出清晰的反射
Reflectance	垂直入射角度下的非金属表面菲涅尔反射率
Emissive	额外的漫反射albedo，用于模拟发光表面
Ambient Occlusion	用于界定表面上一点能够获取多少环境光

为了让我们的标准材质模型更易于使用，我们必须要对其中的三个参数进行重映射：baseColor、roughness、reflectance

8.1 Remapping BaseColor

材质的基础颜色会受到金属度的影响。

对于非金属来说，漫反射所呈现的是其基础色，镜面反射所呈现的是白色。

对于金属来说，不存在漫反射部分，镜面反射所呈现的是其基础色。

所以，在渲染方程中我们不能直接使用基础色，而是需要将其拆解为漫反射颜色与$f_0$。

其中，漫反射颜色的计算相对来说简单直接：

vec3 diffuseColor = (1.0 - metallic) * baseColor.rgb;

8.2 Reflectance

首先我们需要重新说明一下$f_0$的定义：垂直入射角度下的specular reflectance。

我们知道非金属材质同时存在漫反射与镜面反射，而非金属的$f_0$是白色的。故，reflectance的映射我们需要根据材质类别分开讨论。

非金属

对于非金属来说，我们的目标是将$f_0$映射到一个特定的范围上，该范围能够表示常见非金属表面（反射率为$4\%$）与宝石（反射率为$8\%-16\%$）的菲涅尔值。Lagarde在他的论文中所使用的映射函数为：

\[f_0=0.16 \cdot reflectance^2\]

比方说，reflectance为0.5时，所对应的菲涅尔反射率为4%，这对应了现实世界中大多数非金属材质的反射率，所以reflectance的默认值设置为0.5是一个恰当的选择。如下图所示：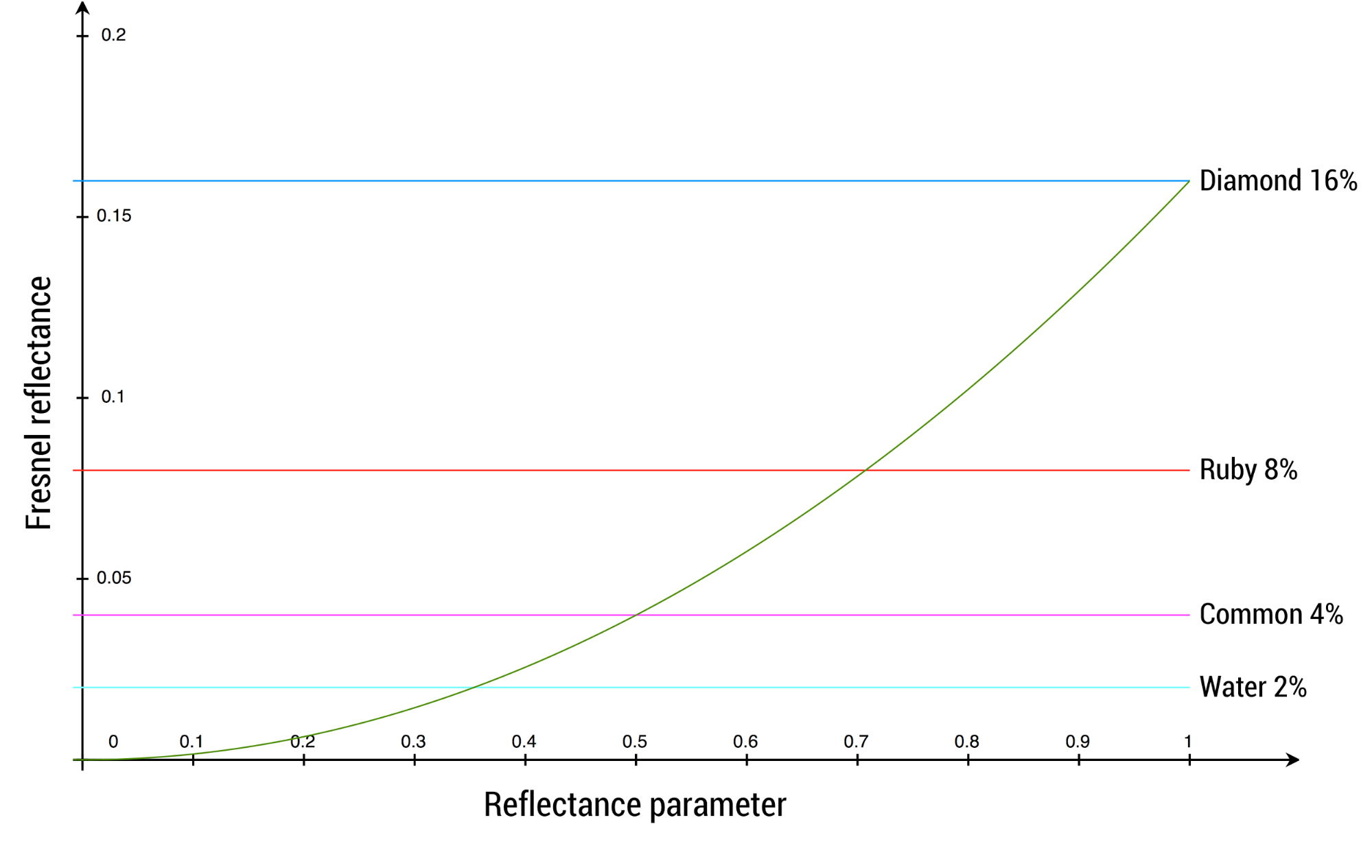

当然，如我们在本章节最开始所提到的，reflectance是用于代替显式的IOR。也就是说，如果某个材质的IOR已知，我们可以通过IOR来计算$f_0$，具体的公式这里就不再展示了。

金属

金属材质的$f_0$是有色的，我们可以直接使用材质的基础色来计算出$f_0$，即：

\[f_0=baseColor \cdot metallic\]

Implement

在标准模型的代码实现中，我们使用以下方式来同时任意金属度下的材质$f_0$：

vec3 f0 = 0.16 * reflectance * reflectance * (1.0 - metallic) + baseColor * metallic;

8.3 Roughness

开发者所设置的粗糙度，被称为感知粗糙度，我们使用以下公式重新映射到感知线性范围：

\[\alpha = perceptualRoughness^2\]

如下图展示了一个银色的金属材质随着粗糙度提高的外观变化，分别使用了映射值（上面）与非映射值（下面）：

很显然，重映射后的粗糙度在美术上是更容易被接受的，如果没有重映射，有光泽的金属表面将不得不被限制在0.0 到 0.05 之间的非常小的范围内。

8.4 Crafting Physically Based Materials

一但我们理解了这四个主要参数的本质含义，我们就能轻松创建出基于物理的材质：

baseColor、metallic、roughness、reflectance

以下是对于上述四个参数的使用建议：

All Materials：

• BaseColor：避免包含任何光照信息，除非是微小的occlusion

Non-Metallic Materials：

• BaseColor：表示材质的漫反射部分所呈现的颜色，需要设置为一个范围在$[30, 240]$之间的sRGB值
• Metallic：0或非常接近与0
• Reflectance：默认为$127$的sRGB值，对应线性的$0.5$与$4\%$的菲涅尔反射率。最低不建议小于线性的$0.35$，该值对应的菲涅尔反射率为$2\%$，在现实世界中几乎没有对应的材质

Metallic Materials：

• BaseColor：表示镜面反射所呈现的颜色与反射率
• Metallic：1或非常接近与1
• Reflectance：直接被忽略，我们会从BaseColor中计算反射率

---

9 Clear Coat Model

目前我们所构建的标准模型非常适合于单层的非各向异性表面。然而在现实世界中，多层材质是非常常见的，特别是在标准层之上有一层薄的半透明层的材质，例如车漆、上漆的木材、亚克力等。

通过添加第二个镜面反射lobe的扩展标准材质模型，我们可以模拟clear coat的材质效果。简单起见，我们将clear coat层定义为非各向异性且非金属的。

由于入射光会穿过clear coat层，我们还需要考虑到能量损失。此外，我们的模型不会考虑光线在层之间的相互反射与折射行为。

9.1 Clear Coat Specular BRDF

清漆层将使用标准模型中使用的相同的 Cook-Torrance 微表面 BRDF 进行建模。由于清漆层始终是各向同性且绝缘的，粗糙度值较低，因此我们可以选择计算成本更低的 DFG 项而不会明显牺牲视觉质量。

对于D与F，我们仍然适用标准模型中的方案，而对于可见性G，我们使用Kelemen模型：

\[V(l, h)=\frac{1}{4(l\cdot h)^2}\]

这个模型并非物理正确，但是在实时渲染中非常合适。

总结来说，我们的clearcoat BRDF是一个基于Cook-Torrance的specular BRDF，使用GGX作为法线分布函数，使用Kelemen可见性函数，以及Schlick菲涅尔函数。

需要注意的是，BRDF中的菲涅尔项需要我们提供$f_0$这个参数，为此，我们假设clear coat层是由聚氨酯这种材料构成的，它与空气的IOR值为1.5，从而我们可以计算出$f_0$为0.04，这也是常见电介质材质的菲涅尔反射率。

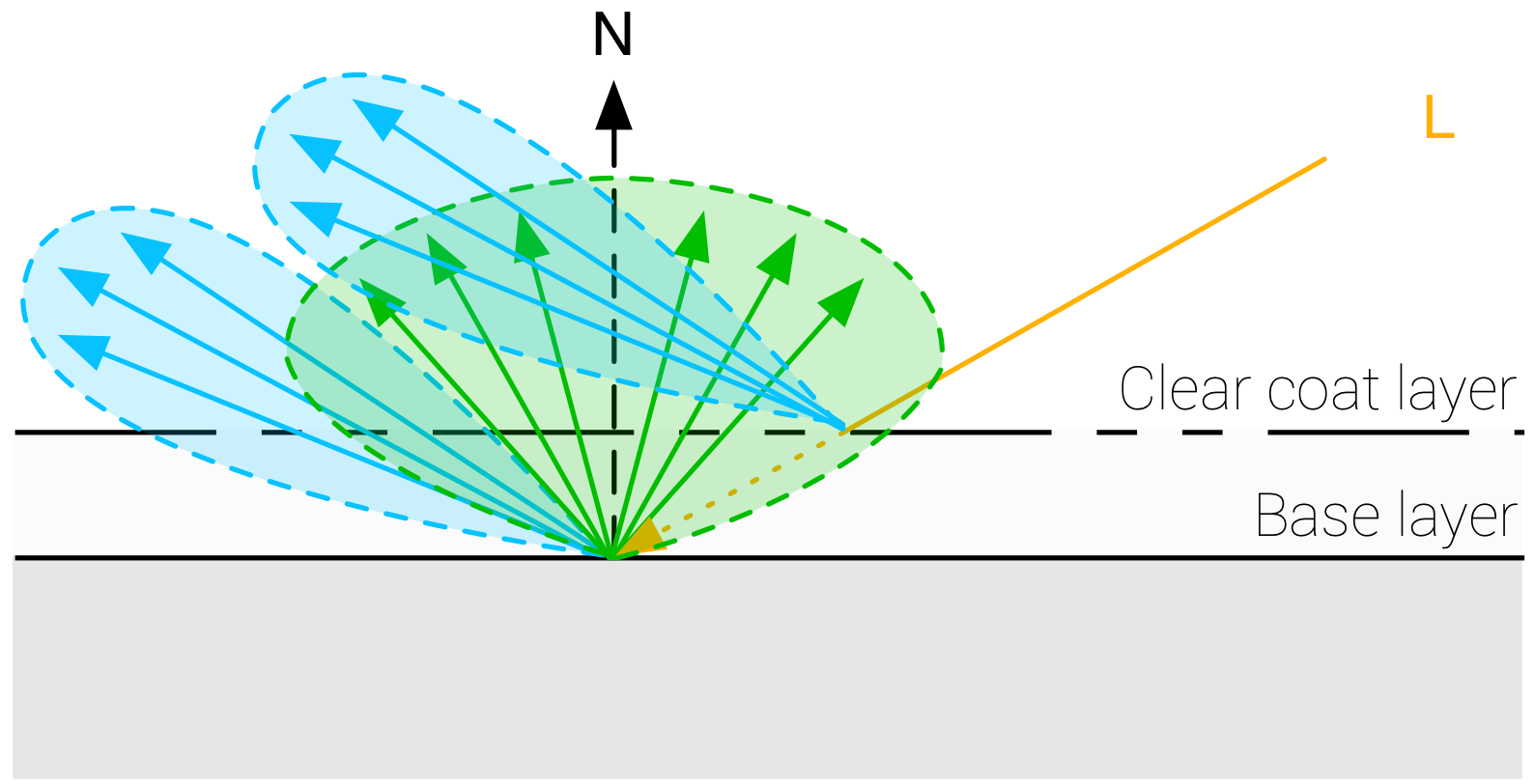
9.2 Integration in the Surface Response

我们需要将因clear coat层而导致的能量损失考虑在内，新的BRDF表达式为：

\[f(v, l)=f_d(v, l)(1-F_c)+f_r(v, l)(1-F_c)+f_c(v, l)\]

其中，$f_c$表示clear coat层的BRDF，$F_c$表示$f_c$的菲涅尔项

9.3 Clear coat Parameterization

清漆材质在标准材质的基础上，多了两个额外的参数：

• ClearCoat：清漆层的强弱
• ClearCoatRoughness：感知粗糙度

最终，加入清漆层的BRDF实现代码为：

void BRDF(...) {
    // compute Fd and Fr from standard model

    // remapping and linearization of clear coat roughness
    clearCoatPerceptualRoughness = clamp(clearCoatPerceptualRoughness, 0.089, 1.0);
    clearCoatRoughness = clearCoatPerceptualRoughness * clearCoatPerceptualRoughness;

    // clear coat BRDF
    float  Dc = D_GGX(clearCoatRoughness, NoH);
    float  Vc = V_Kelemen(clearCoatRoughness, LoH);
    float  Fc = F_Schlick(0.04, LoH) * clearCoat; // clear coat strength
    float Frc = (Dc * Vc) * Fc;

    // account for energy loss in the base layer
    return color * ((Fd + Fr * (1.0 - Fc)) * (1.0 - Fc) + Frc);
}

9.4 Base Layer Modification

由于清漆层的存在，标准材质不再与空气相接触，而是与清漆材质相接触，所以我们需要重新计算标准材质的$f_0$。由于清漆材质的$f_0$是已知的，所以这一步不难实现。

\[f_{0_{base}} = \frac{\left( 1 - 5 \sqrt{f_0} \right) ^2}{\left( 5 - \sqrt{f_0} \right) ^2}\]

---

10 Anisotropic Model

前面描述的标准材质模型只能描述各向同性的表面，即各个方向上的属性都相同的表面。然而，许多现实世界中的材料，如拉丝金属，只能使用各向异性模型来复现。

10.1 Anisotropic Specular BRDF

我们可以修改此前的各项同性的镜面反射BRDF来匹配各向异性材质，Burley使用了一个各向异性的GGX法线分布函数：

\[D_{aniso}(h, \alpha)=\frac{1}{\pi\alpha_t \alpha_b}\cdot\frac{1}{((\frac{t\cdot h}{\alpha_t})^2+(\frac{b\cdot h}{\alpha_b})^2+(n\cdot h)^2)}\]

可以发现，这个法线分布函数依赖于两个粗糙度参数，分别为副切线与切线方向上的粗糙度。这两个值可以通过粗糙度与一个额外的各向异性参数推导出来。具体的推导方式有很多，我们选择Kulla的方案，该方案在创建清晰高光的同时，计算成本也很低：

\[\begin{align*} \alpha_t &= \alpha \times (1 + anisotropy) \\ \alpha_b &= \alpha \times (1 - anisotropy) \end{align*}\]

对应的代码实现为：

float at = max(roughness * (1.0 + anisotropy), 0.001);
float ab = max(roughness * (1.0 - anisotropy), 0.001);

float D_GGX_Anisotropic(float NoH, const vec3 h, const vec3 t, const vec3 b, float at, float ab) {
    float ToH = dot(t, h);
    float BoH = dot(b, h);
    float a2 = at * ab;
    highp vec3 v = vec3(ab * ToH, at * BoH, a2 * NoH);
    highp float v2 = dot(v, v);
    float w2 = a2 / v2;
    return a2 * w2 * w2 * (1.0 / PI);
}

此外，Heitz也提出了各向异性的masking-shadowing函数，且能够匹配高度矫正的GGX分布：

对应的实现为：

float at = max(roughness * (1.0 + anisotropy), 0.001);
float ab = max(roughness * (1.0 - anisotropy), 0.001);

float V_SmithGGXCorrelated_Anisotropic(float at, float ab, float ToV, float BoV,
        float ToL, float BoL, float NoV, float NoL) {
    float lambdaV = NoL * length(vec3(at * ToV, ab * BoV, NoV));
    float lambdaL = NoV * length(vec3(at * ToL, ab * BoL, NoL));
    float v = 0.5 / (lambdaV + lambdaL);
    return saturateMediump(v);
}

10.2 Anisotropic Parameterization

Anisotropy参数的范围在$[-1, 1]$之间，表示材质各向异性的量

---

11 Subsurface Model

[TODO]

---

12 Cloth Model

前面所描述的所有材质模型都是为了模拟致密的表面而设计的，无论是在宏观层面还是微观层面。然而，衣服和织物通常是由松散连接的threads线组成的，这些线会吸收和散射入射光。

由于早期提出的微表面双向反射分布函数（BRDF）基于表面由随机凹槽组成且表现为完美镜子的假设，所以在重现布料的性质方面表现不佳。与硬表面相比，布料的特点是具有更柔和的镜面高光区域和较大的衰减，以及由正向 / 反向散射引起的模糊光照。一些织物还呈现出双色镜面颜色（例如天鹅绒）。

天鹅绒是布料材质模型的一个有趣用例。如下图所示，这种类型的织物由于正向和反向散射而呈现出强烈的边缘光。这些散射现象是由垂直于织物表面的纤维引起的。当入射光来自与观察方向相反的方向时，纤维会向前散射光线。类似地，当入射光来自与观察方向相同的方向时，纤维会向后散射光线。

12.1 Cloth Specular BRDF

在Ashikhmin与Premoze的理论中，用于模拟天鹅绒的布料BRDF中最重要的是法线分布函数，而shadowing-masking项相对来说没那么关键。他们所使用的NDF是一个反向的高斯分布，这有助于实现因前向反向散射而带来的模糊光照，此外，他们还使用了一个额外的偏移量，用于模拟front-facing specular贡献值。最终，我们所使用的NFD的数学表达式如下：

\[D_{velvet}(v,h,\alpha)=\frac{1}{\pi(1+4\alpha^2)}(1+4\frac{exp\big( \frac{-cot^2\theta_h}{\alpha^2} \big)}{sin^4\theta_h})\]

最终，完整的specular BRDF的数学表达式为：

\[f_r(v,h,\alpha=\frac{D_{velvet}(v,h,\alpha)}{4(n\cdot l+n\cdot v-(n\cdot l)(n\cdot v))}\]

从数学表达式中可以发现：

• 使用了一个更平滑的值作为分母
• 移除了菲涅尔部分

此外，Estevez与Kulla提出了另一个NDF，被称为Charlie NDF，它基于指数正弦曲线。该实现方式的优点在于，提供了更柔和的外观，并且其实现过程更简单：

\[D(m)=\frac{(2+\frac{1}{\alpha})sin(\theta)^{\frac{1}{\alpha}}}{2\pi}\]

12.1.1 Sheen Color

为了更好地控制布料的外观并使用户能够重新创建双色调镜面反射材质，我们引入了直接修改镜面反射率的功能。下图显示了使用我们称为 “sheen color” 的参数的示例。

12.2 Cloth Diffuse BRDF

Cloth BRDF的漫反射部分依然基于Lambertian模型，但是我们对其进行了一定的修改，使其能够遵循能量守恒定律，并额外提供了一个可选的次表面散射项。这个次表面散射项并非基于物理，但可以用于模拟特定类型布料的散射、部分吸收的外观。

不包含额外的次表面散射的漫反射项的数学表达式如下：

\[f_d(v,h)=\frac{c_{diff}}{\pi}(1-F(v,h))\]

其中，$F(v,h)$是我们在cloth specular BRDF中所使用的菲涅尔项。而在实际的代码实现中，我们选择删去这一部分。

最终，cloth BRDF的代码实现为：

// specular BRDF
float D = distributionCloth(roughness, NoH);
float V = visibilityCloth(NoV, NoL);
vec3  F = sheenColor;
vec3 Fr = (D * V) * F;

// diffuse BRDF
float diffuse = diffuse(roughness, NoV, NoL, LoH);
#if defined(MATERIAL_HAS_SUBSURFACE_COLOR)
// energy conservative wrap diffuse
diffuse *= saturate((dot(n, light.l) + 0.5) / 2.25);
#endif
vec3 Fd = diffuse * pixel.diffuseColor;

#if defined(MATERIAL_HAS_SUBSURFACE_COLOR)
// cheap subsurface scatter
Fd *= saturate(subsurfaceColor + NoL);
vec3 color = Fd + Fr * NoL;
color *= (lightIntensity * lightAttenuation) * lightColor;
#else
vec3 color = Fd + Fr;
color *= (lightIntensity * lightAttenuation * NoL) * lightColor;
#endif

12.3 Cloth Parameterization

与标准材质相比，布料不使用metallic与reflectance这两个参数，而是使用另外两个额外的参数：

• SheenColor：用于创建two-tone specular fabric效果的specular tint，默认为0.04
• SubsurfaceColor：散射与吸收发生后的漫反射颜色

To create a velvet-like material, the base color can be set to black (or a dark color). Chromaticity information should instead be set on the sheen color.

To create more common fabrics such as denim, cotton, etc. use the base color for chromaticity and use the default sheen color or set the sheen color to the luminance of the base color.