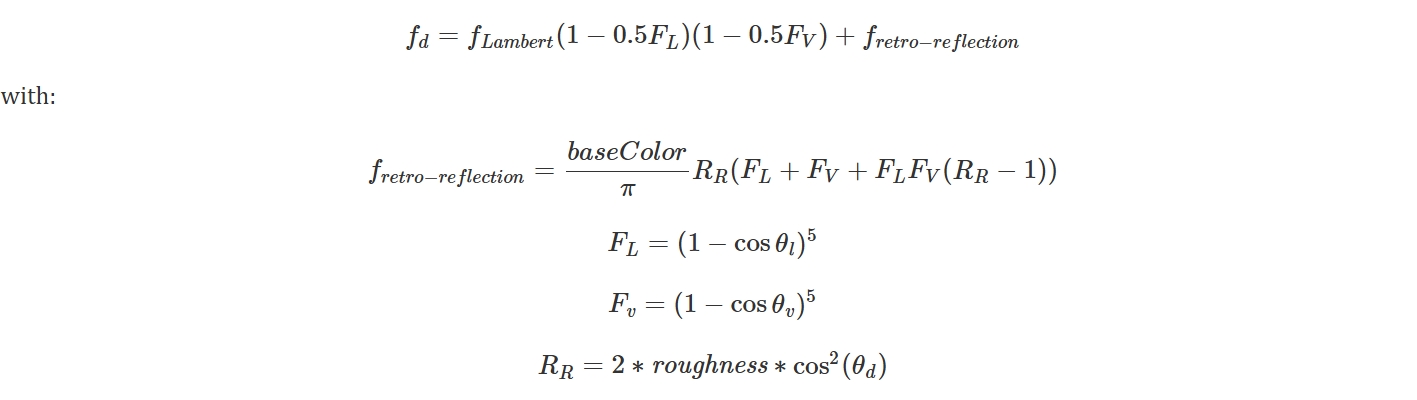Physically Based Shading at Disney

1 The Microfacet Model

各向同性材质的微表面模型的通用形式如下：

\[f(l, v)=\text{diffuse}+\frac{D(h_\theta)F(\theta_h)G(\theta_l, \theta_v)}{4cos\theta_l cos\theta_v}\]

其中，$\text{diffuse}$项有多种形式，通常会使用Lambertian模型并以常数表示。而对于镜面反射项：

• D表示微表面的分布函数，决定specular peak的形状
• G表示几何衰减
• F表示菲涅尔反射系数

$\theta_l$与$\theta_v$分别表示入射光线与观察方向相对于法线的夹角，$\theta_h$则表示半程向量与法线的夹角。$\theta_d$表示观察方向与半程向量之间的夹角。

2 Disney “Principled” BRDF

2.1 Principles

• 采用直观参数而非物理量参数
• 参数数量最小化
• 参数合理范围限定在$[0, 1]$区间
• 允许在特定场景下突破合理范围限制
• 所有参数组合需保证稳定合理的输出

2.2 Parameters

• baseColor：表面颜色，通常有纹理贴图提供
• subsurface：使用此表面近似来控制漫反射形状
• metallic：金属度，用于再两个不同模型之前做线性插值。金属材质模型不包含漫反射分量，其镜面反射的入射着色与基础色相同
• specular：入射镜面反射量，该参数用于替代显式IOR定义
• specularTint：使入射镜面反射趋向基础色着色，掠射镜面仍保持无色
• roughness：表面粗糙度，同时影响漫反射与镜面反射
• anisotropic：各向异性强度，0=各向同性，1=最大各向异性
• sheen：附加掠射反射分量，专为布料材质设计
• sheenTint：布料光泽趋向基础色的着色强度
• clearcoat：第二层特殊用途的镜面反射波瓣
• clearcoatGloss：控制清漆层光泽度（0=缎面质感，1=镜面质感）

2.3 Diffuse Model Details

Lambert漫反射模型在边缘区域常显过暗，加入菲涅尔因子提升物理合理性后反而加剧暗部问题。基于此，我们开发了新型经验式漫反射逆向反射模型，该模型实现了平滑表面的漫反射菲涅尔阴影与粗糙表面附加高光之间的自然过渡。其物理机制可解释为：粗糙表面光线在微结构侧边发生进出折射，导致掠射角透射率提升。该模型既延续了特设模型的艺术可控性，又具备更合理的物理基础。

在这个模型中，我们忽略了漫反射菲涅尔因子的IOR，并且假设不存在入射漫反射的能量损失，这允许了我们直接指定入射漫反射颜色。此外。本模型还使用Schlick菲涅尔近似，并将将掠射逆向反射终点值绑定粗糙度参数（而非归零）。数学表达式如下：

\[f_d=\frac{baseColor}{\pi}(1+(F_{D90}-1)(1-cos\theta_l)^5)(1+(F_{D90}-1)(1-cos\theta_v)^5)\]

其中，

\(F_{D90}=0.5+2*roughness*cos^2\theta_d\) 该模型生成的漫反射菲涅尔阴影可产生如下效果：光滑表面在掠射角处的漫反射率降低0.5倍，粗糙表面则增强至2.5倍。

我们的次表面参数融合了基础漫反射形态与受Hanrahan-Krueger次表面BRDF启发的模型。该机制适用于为远距离物体或平均散射路径较短的物体赋予次表面外观；然而，它无法替代完整的次表面传输计算，因其无法模拟光线渗入阴影或穿透表面的光扩散效应。

2.4 Specular D Details

在主流模型中，GGX拥有最长的衰减尾部。该模型实际上等同于Trowbridge-Reitz分布。然而，对于许多材质而言，这种分布的尾部长度仍显不足。

Trowbridge与Reitz将其提出的分布函数与多种其他分布同磨砂玻璃的测量数据进行对比。其中，Berry模型的数学形式与Trowbridge-Reitz极为相似，但其指数项为1而非2，从而生成更长的衰减尾部。这启发我们引入一个含可变指数的广义分布——称为广义Trowbridge-Reitz（GTR）分布：

\[D_{GTR}=c/(\alpha^2cos^2\theta_h+sin^2\theta_h)^\gamma\]

其中，$c$表示一个缩放常量，$\alpha$是一个范围在$[0, 1]$的粗糙度参数。

一个合理的微表面分布必须满足归一化条件，且为实现高效渲染需支持重要性采样。这两点均要求该分布可在半球空间内积分。幸运的是，此分布函数具有简单的闭合积分形式。

在我们的BRDF设计中，采用双固定高光波瓣结构，均基于GTR模型：主波瓣使用γ=2（对应GGX分布），次波瓣使用γ=1（Berry长尾分布）。主波瓣表征基础材质属性，支持各向异性与金属度调节；次波瓣模拟表层清漆效果，强制各向同性且非金属。

通过将粗糙度参数映射为$\alpha=roughenss^2$，实现感知线性变化，避免插值失真。该设计可精准匹配光滑材质表现，并提供自然的材质过渡效果。

我们使用specular参数替代显式IOR参数来确定入射高光量。该参数的归一化范围被线性重新映射到入射高光范围$[0.0, 0.08]$，这对应着折射率IOR在$[1.0, 1.8]$范围内的数值，涵盖了大多数常见材质。值得注意的是，参数范围的中间值对应IOR为1.5，这是一个非常典型的数值，也是我们的默认设置。这种参数映射方式极大帮助美术师创建可信材质，因为现实世界中的入射反射率数值之低往往与直觉相悖。

对于我们的清漆层，我们采用固定的$1.5$IOR来代表聚氨酯材质，转而允许美术师通过clearcoat参数调节该层的整体强度。归一化参数范围对应整体强度缩放系数$[0.0, 0.25]$。尽管该层对视觉效果影响显著，但其能量占比相对较小，因此无需从基础层扣除能量。当参数设为0时，清漆层将被完全禁用且不产生性能开销。

2.5 Specular F Details

Schlick菲涅尔近似已足够满足需求，且比完整菲涅尔方程简单得多；该近似引入的误差显著小于其他因素造成的误差。其数学表达式为：

\[F_{Schlick}=F_0+(1-F_0)(1+cos\theta_d)^5\]

其中，$F_0$表示法线入射时的镜面反射率，对于电介质是非彩色的，而对金属是彩色的。其实际数值取决于折射率。需注意，镜面反射来源于微表面，因此菲涅尔项$F$依赖于光线向量与微表面法线（即半角向量）之间的夹角d，而非光线与宏观表面法线的入射角。 菲涅尔函数可视为在法线入射反射率与掠射角下的全反射（值为1）之间进行非线性插值。

2.6 Specular G Details

在我们的模型中采用了混合方案。鉴于主高光已使用Smith遮蔽因子，我们采用Walter为GGX推导的G项，但通过重映射粗糙度来降低高光表面的极端增益。具体而言，在计算G项时，我们将原始粗糙度从[0,1]范围线性缩放到[0.5,1]的限定范围。注意：此操作在先前所述的粗糙度平方之前进行，因此最终g值为(0.5 + roughness/2)²。

此重映射方案基于实测数据对比及美术师反馈——低粗糙度时高光过强的问题。调整后的G函数实现了随粗糙度变化、至少部分物理可信的表现。对于清漆层高光，我们未采用Smith G推导，而是直接使用固定粗糙度0.25的GGX G函数，经验证该方案在物理合理性与艺术表现力间取得平衡。

---

3 Implements in Unity SRP Project

3.1 Sheen

sheen lobe是所有项中相对来说最简单的一项。这是一个独立的lobe，基于sheen参数，该lobe的颜色会在白色与基于sheenTint参数的特定颜色之间进行插值，最后再加到其他lobe上。

sheen lobe的意义在于，模拟表面掠射角的光线行为，主要用于布料类材质的逆向反射或粗糙表面，以补偿仅建模单次散射的几何项导致的能量损失。

在迪士尼的BRDF实现中，sheen tint并非直接使用了Base Color，而是通过线性空间下的CIE亮度权重计算亮度值，并进行归一化处理，简单来说，就是从base color中提取色相与饱和度：

float3 CalculateTint(float3 baseColor)
{
    float luminance = Dot(float3(0.3f, 0.6f, 1.0f), baseColor);
    return (luminance > 0.0f) ? baseColor * (1.0f / luminance) : float3::One_;
}

sheen lobe的数学表达式如下：

\[f(sheen, \theta_d)=sheen * ((1-sheenTint)+sheenTint*tint)*(1-cos\theta_d)^5\]

对应的代码实现为：

static float3 EvaluateSheen(const SurfaceParameters& surface, const float3& wo, const float3& wm, const float3& wi)
{
    if(surface.sheen <= 0.0f) {
        return float3::Zero_;
    }

    float dotHL = Dot(wm, wi);
    float3 tint = CalculateTint(surface.baseColor);
    return surface.sheen * Lerp(float3(1.0f), tint, surface.sheenTint) * Fresnel::SchlickWeight(dotHL);
}

3.2 Clearcoat

clearcoat lobe是另一个附加的lobe，其强度由clearcoat参数控制，形状由clearcoatGloss参数控制。该lobe的实现稍显复杂，虽然建模了完整的BRDF，但固定了大部分参数项以确保其成为美术友好的、用于模拟材质表面透明涂层的简易方案。

clearcoat使用的法线分布项采用Burley提出的“广义Trowbridge-Reitz”(GTR)固定形式BRDF，其归一化形式采用固定gamma=1参数：

\[D_{GTR_1}=\frac{\alpha^2-1}{\pi log(\alpha^2)}\cdot \frac{1}{1+(\alpha^2-1)cos^2\theta_h}\]

菲涅尔项采用Schlick近似，并固定折射率为1.5以代表聚氨酯材质。经计算得出$F_0=0.04$：

\[F_{Schlick}=F_0+(1-F_0)(1-cos\theta_h)^5\]

清漆层使用的遮蔽-阴影项采用可分形式的Smith GGX模型，并固定粗糙度为0.25。尽管该项与法线分布的理论匹配性不足，但因其视觉效果已足够理想，故未做调整。

\[\begin{aligned} G(\theta,\alpha)=\frac{1}{cos\theta+\sqrt{\alpha^2+cos\theta-\alpha^2cos^2\theta}}\\ G(\theta_l, \theta_v)=G(\theta_l, 0.25)*G(\theta_v, 0.25) \end{aligned}\]

对应的代码实现为

//===================================================================================================================
static float GTR1(float absDotHL, float a)
{
    if(a >= 1) {
        return InvPi_;
    }

    float a2 = a * a;
    return (a2 - 1.0f) / (Pi_ * Log2(a2) * (1.0f + (a2 - 1.0f) * absDotHL * absDotHL));
}

//===================================================================================================================
float SeparableSmithGGXG1(const float3& w, float a)
{
    float a2 = a * a;
    float absDotNV = AbsCosTheta(w);

    return 2.0f / (1.0f + Math::Sqrtf(a2 + (1 - a2) * absDotNV * absDotNV));
}

//===================================================================================================================
static float EvaluateDisneyClearcoat(float clearcoat, float alpha, const float3& wo, const float3& wm,
                                     const float3& wi, float& fPdfW, float& rPdfW)
{
    if(clearcoat <= 0.0f) {
        return 0.0f;
    }

    float absDotNH = AbsCosTheta(wm);
    float absDotNL = AbsCosTheta(wi);
    float absDotNV = AbsCosTheta(wo);
    float dotHL = Dot(wm, wi);

    float d = GTR1(absDotNH, Lerp(0.1f, 0.001f, alpha));
    float f = Fresnel::Schlick(0.04f, dotHL);
    float gl = Bsdf::SeparableSmithGGXG1(wi, 0.25f);
    float gv = Bsdf::SeparableSmithGGXG1(wo, 0.25f);

    fPdfW = d / (4.0f * absDotNL);
    rPdfW = d / (4.0f * absDotNV);

    return 0.25f * clearcoat * d * f * gl * gv;
}

3.3 Specular BRDF

Specular BRDF采用传统的Cook-Torrance微表面模型，使用各向异性GGX（即GTR2）分布配合Smith遮蔽-阴影函数。Burley计算各向异性权重的方法如下：

\[\begin{aligned} aspect=\sqrt{1-0.9*anisotropic}\\ \alpha_x=roughness^2/aspect\\ \alpha_y=roughness^2*aspect \end{aligned}\]

法线分布函数的数学表达式如下：

\[D_{GTR_{2aniso}}=\frac{1}{\pi\alpha_x\alpha_y}\cdot\frac{1}{(\frac{(h\cdot x)^2}{\alpha^2_x}+\frac{(h\cdot y)^2}{\alpha^2_y}+(h\cdot n)^2)^2}\]

迪士尼将其几何项调整为匹配Heitz在论文中推导的各向异性Smith GGX项：

\[\begin{aligned} G1_{GTR_{2aniso}}=\frac{1}{1+\Lambda(\hat\omega_o)}\\ \Lambda(\hat\omega_o)=\frac{-1+\sqrt{1+\frac{1}{a^2}}}{2}\\ a=\frac{1}{tan\theta_o\sqrt{cos^2\phi_o\alpha^2_x+sin^2\theta_o\alpha_y^2}} \end{aligned}\]

对应的代码实现为如下。如代码所示，我们通过调用DisneyFresnel()以计算菲涅尔项，我们会在后面聊到这个函数

//===================================================================================================================
float GgxAnisotropicD(const float3& wm, float ax, float ay)
{
    float dotHX2 = Square(wm.x);
    float dotHY2 = Square(wm.z);
    float cos2Theta = Cos2Theta(wm);
    float ax2 = Square(ax);
    float ay2 = Square(ay);

    return 1.0f / (Math::Pi_ * ax * ay * Square(dotHX2 / ax2 + dotHY2 / ay2 + cos2Theta));
}

//===================================================================================================================
float SeparableSmithGGXG1(const float3& w, const float3& wm, float ax, float ay)
{
    float dotHW = Dot(w, wm);
    if (dotHW <= 0.0f) {
        return 0.0f;
    }

    float absTanTheta = Absf(TanTheta(w));
    if(IsInf(absTanTheta)) {
        return 0.0f;
    }

    float a = Sqrtf(Cos2Phi(w) * ax * ax + Sin2Phi(w) * ay * ay);
    float a2Tan2Theta = Square(a * absTanTheta);

    float lambda = 0.5f * (-1.0f + Sqrtf(1.0f + a2Tan2Theta));
    return 1.0f / (1.0f + lambda);
}

//===================================================================================================================
static float3 EvaluateDisneyBRDF(const SurfaceParameters& surface, const float3& wo, const float3& wm,
                                 const float3& wi, float& fPdf, float& rPdf)
{
    fPdf = 0.0f;
    rPdf = 0.0f;

    float dotNL = CosTheta(wi);
    float dotNV = CosTheta(wo);
    if(dotNL <= 0.0f || dotNV <= 0.0f) {
        return float3::Zero_;
    }

    float ax, ay;
    CalculateAnisotropicParams(surface.roughness, surface.anisotropic, ax, ay);

    float d = Bsdf::GgxAnisotropicD(wm, ax, ay);
    float gl = Bsdf::SeparableSmithGGXG1(wi, wm, ax, ay);
    float gv = Bsdf::SeparableSmithGGXG1(wo, wm, ax, ay);

    float3 f = DisneyFresnel(surface, wo, wm, wi);

    Bsdf::GgxVndfAnisotropicPdf(wi, wm, wo, ax, ay, fPdf, rPdf);
    fPdf *= (1.0f / (4 * AbsDot(wo, wm)));
    rPdf *= (1.0f / (4 * AbsDot(wi, wm)));

    return d * gl * gv * f / (4.0f * dotNL * dotNV);
}

你会注意到在可分式Smith GGX G1函数中，我使用了大量三角函数（例如Sin2Phi、TanTheta）。这里采用的是《理解基于微表面的BRDF中遮蔽-阴影函数》论文中描述的未优化实现。迪士尼BRDF探索器中存在该函数的优化版本，但在某些情况下会导致无限值，因此我不确定其正确性。

3.5 Specular BSDF

[略]

3.6 Diffuse BRDF

diffuse lobe相比传统的Lambert模型更为复杂。Burley为适配MERL材质数据库进行了大量改进，其模型包含漫反射菲涅尔因子及逆向反射项。此外，模型中的非方向性部分被解耦，以便通过漫射或体散射模型实现次表面替换。完整的漫反射波瓣表达式为：