Crash Course in BRDF Implementation
1 Introduction
在本篇博客中,我们将会介绍游戏领域中常用的一些基础BRDF的实现,以及它们背后的原理。
2 So, What is the BRDF?
双向反射分布函数(BRDF)描述了表面在特定入射光方向和出射光方向组合下的反射特性。具体来说,它决定了当一定量的光线从某个方向入射时,材料表面会向特定方向反射多少光能,这一特性取决于材料表面的属性。例如,对于漫反射表面,BRDF显示所有方向都有少量均匀反射;而镜面则会将所有入射光精确反射至单一方向。
这种数学表述具有高度灵活性,使我们可以将材料表面的光学响应封装在BRDF实现及其参数设置中,从而使其独立于底层的光传输算法。值得注意的是,BRDF并不区分直接入射光和间接入射光,这意味着它既可以用于计算场景中虚拟光源的直接光照贡献(局部光照),也可以计算经过其他表面一次或多次反射的间接光照贡献(全局光照)。这种特性也意味着BRDF的实现独立于光源的具体实现方式——光源只需提供着色点的入射光方向和强度参数即可。
渲染算法与光照的解耦性,意味着我们可以将抽象的BRDF实现为“材质插件”,并通过简洁的API进行调用,从而确保不同的渲染器生成一致的视觉效果。
基于物理的BRDF需要满足以下原则:
- Helmholtz Reciprocity:交换入射方向与反射方向,计算得到的reflectance结果一致。这也是B(bidirectional)的由来。
- Energy Conservation:表面所反射的能量小于等于接收的能量
例如Phong这样的早期经验模型通常不满足上述原则,所以不适用于写实渲染,也无法正确模拟很多材质的表现,例如粗糙表面或金属,我们会在后面更详细地讨论这部分内容。
需要指出的是,部分成功应用的BRDF模型并不完全满足理论要求。例如,迪士尼模型未严格遵循能量守恒原则),而Autodesk模型则可能违反亥姆霍兹互易性。实际上,完美的能量守恒也未必是强制要求——只要BRDF不产生能量增益(即反射光能不超过入射光能),即便存在能量损耗导致表面亮度降低,通常也不会造成严重问题。最终,在渲染内容完全可控的前提下,BRDF实现的高性能与艺术家操作的便捷性,往往比满足所有理论约束更为重要。
2.1 Construction of BRDF
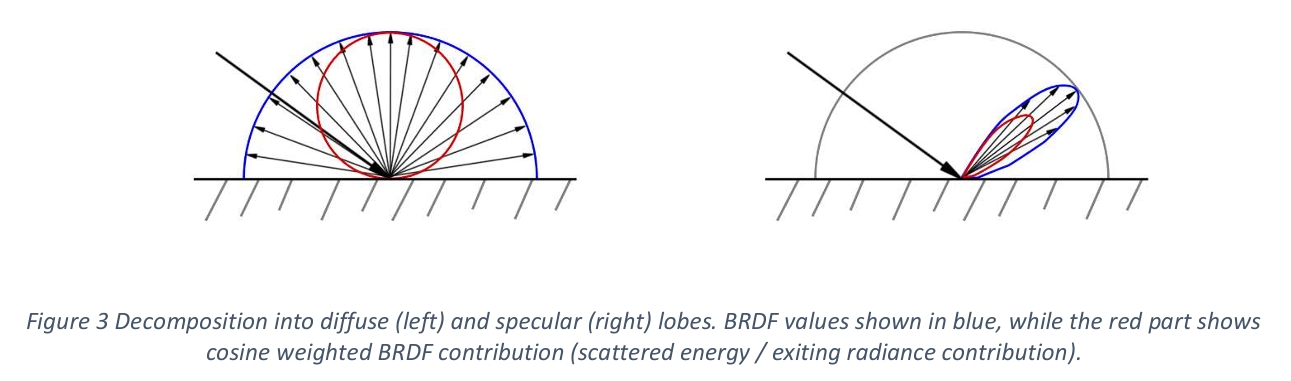
在游戏领域,大多数BRDF模型由漫反射与高光反射两个波瓣组成。这种分解源于光线与表面的物理交互过程:当光线撞击表面时,部分被直接反射(形成高光反射BRDF),其余部分则散射进入材质内部。在材质深层,光线经历次表面散射作用,部分能量最终会再次到达表面并以随机方向射出(形成漫反射BRDF)。由于在材质内部的散射作用,这部分光线会被”光谱过滤”,赋予物体特定的颜色表现。值得注意的是,光线在次表面传播过程中会产生空间扩散效应,导致入射点与出射点位置分离,从而形成典型的次表面散射现象。但在实际游戏渲染中,通常采用简化模型——直接假定入射点与出射点位置重合,忽略次表面散射的空间传播特性。这种折中方案在保证实时渲染效率的同时,仍能有效模拟大多数材质的视觉特征。
光线在表面发生反射或散射的比例由菲涅耳方程描述。当光线以掠射角入射时,其反射概率显著增加,这种现象被称为”菲涅耳反射效应”,如下图所示。菲涅耳项还负责模拟金属与非金属材料的本质区别:金属具有远高于电介质的吸收系数,导致部分本应反射的光线被材料吸收。由于这种吸收具有波长依赖性,某些金属(如黄金)的反射光会呈现出与吸收波长相关的色彩特征,而电介质材料的反射光则基本保持光源的原始颜色。关于菲涅耳项的详细讨论将在4.3节展开。
需要特别指出的是,由于构成漫反射BRDF的光线经历了两次穿越材质表面(入射与出射),理论上应对其应用两次菲涅耳衰减作用。但在实际材质计算中,漫反射BRDF在设计时通常会内建这种双重衰减的补偿机制——或通过能量守恒约束自动实现该特性,或直接将其整合至漫反射率参数的计算逻辑中。这种工程化的处理方式使得美术人员在调节材质时无需手动计算两次菲涅耳效应,从而简化了工作流程,同时确保物理合理性与视觉表现的一致性。
3 Implementing Simple BRDFs
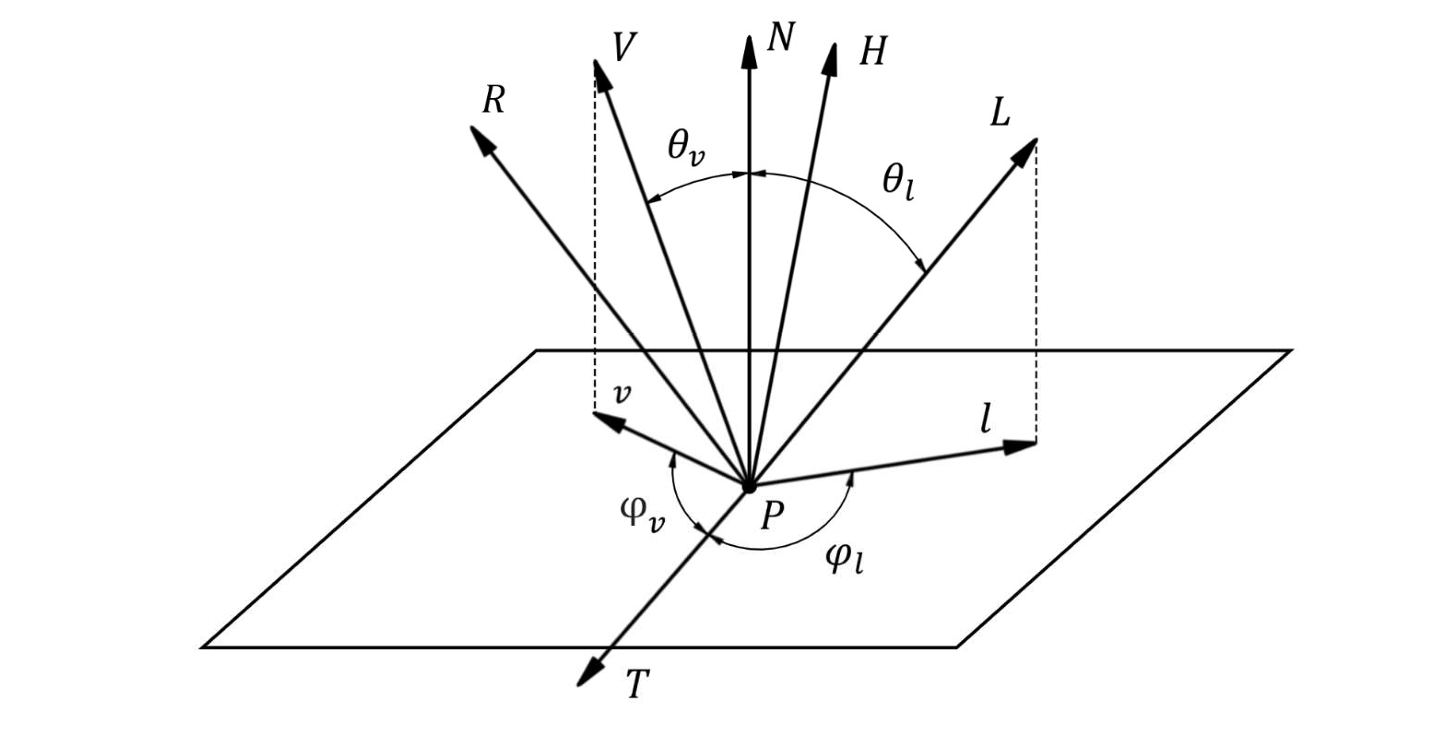
本节将重点解析经典基础BRDF模型——包括兰伯特(Lambertian)反射模型、冯氏(Phong)高光模型等,并建立统一的接口规范,为后续更复杂的BRDF实现提供即插即用替换模块的技术框架。在具体展开前,我们需借助下图明确定义若干关键几何向量(所有向量默认是归一化的):
- $N$:源自表面几何法线或法线贴图,决定表面微观朝向。当使用法线贴图时,N可能显著偏离几何法线,实现细节增强的凹凸效果。
- $V$:由着色点指向相机位置的向量
- $L$:指向场景光源的向量
- $H$:由
H = normalize(V + L)计算获得,表示$V$与$L$的角平分线方向,同时也对应于使入射光沿$V$方向完美反射的微表面法线 - $R$:通过反射公式
R = reflect(-L, N)生成,表示入射光$L$关于法线$N$的理想镜面反射方向 - $T$:位于三角形平面内且与法线$N$正交的切向量
3.1 Lambertian Diffuse BRDF
Lambertian是最简单的漫反射BRDF函数之一,它假设入射光在所有可能方向(表面法线周围的半球空间内)均匀散射。尽管这个模型相对简单,但它能很好地近似许多现实材质的漫反射特性,且计算效率极高。因此,这种模型非常适合作为次级光线反射的计算方案(需配合合适的高光BRDF使用),同时也是UE4中默认的漫反射BRDF实现。由于Lambertian模型不依赖观察视角,它能够完美兼容基于时间累积和重投影的算法(如降噪、TAA等)。其数学表达式为:
\[f_{\text{Lambertian(L, V)}} = \frac{\text{Diffuse Reflectance}}{\pi}\]对于已知方向$L$的光源向相机方向的反射的计算,可以通过以下方式实现:
1
brdfLambertian = (diffuseReflectance / PI) * dot(N, L);
通过这种方式,我们实现了BRDF接口中被称为eval的函数。需要注意的是,我们将渲染方程中的cosine项移至了我们的eval函数。这是一种常见的做法,因为在某些情况下,该cosine项可能会与BRDF中所使用的另一个cosine项相互抵消。我们的这种实现方式可以被称为“内置cosine项的BRDF”,此时就需要注意不要重复应用cosine项。
此外,diffuseReflectance(通常记作$\rho$)决定了入射光线在漫反射波瓣中的反射比例,通常有我们在后续所讨论的“base color”参数计算得出。有时我们也会使用albedo这个术语,但该术语可能存在歧义——严格来说,albedo(定义为入射光与反射光的比例)可能具有反向相关性,但在实际应用中,通常特指光线以法线入射方向下的数值。
另一个常见的优化手段是,将除以常数$\pi$的操作移至预处理阶段,也就是对diffuse reflectance纹理进行预除操作。但这样的话,我们需要对所有使用diffuse reflectance的相关函数都进行相应的调整,其中部分函数可能原本并未包含除以$\pi$的操作。或者,我们也可以对光照强度进行预除,但这种方法并不适用于路径追踪这种光线可能通过多次反射而传播的场景。所以,为了避免混淆,我们将除以$\pi$的操作直接集成在BRDF的内部实现中。
目前为止,我们可以使用eval函数计算来自已知方向的光线对BRDF的贡献。对于大多数光线传输算法(例如蒙特卡洛路径追踪),还需要另一个函数来确定下一条光线应追踪的方向。我们将此函数命名为sample。该函数以随机数作为参数,返回一个新的光线方向,以及概率密度函数(PDF)的值。PDF可理解为选择该特定方向相对于其他可能方向的概率权重。
在蒙特卡洛估值器中,我们有:
\[F=\frac{f(x)}{pdf(x)}\]如果代入Lambertian BRDF函数,则有:
\[I=\frac{f_{Lambertian}(L,V)}{pdf(L)}\]即:
\[I=\frac{\frac{diffuse reflectance}{\pi}(N\cdot L)}{pdf(L)}\]其中,我们将$I$的值称为采样权重,而$pdf$的值这取决于我们选择的采样方式。通过选择恰当的采样方式,我们有可能抵消掉BRDF中的某些项,从而减少计算量。在本博客中,我们选择的cosine-weighted hemisphere采样方式适用于Lambertian以及其他漫反射BRDF,即$pdf = \frac{(N\cdot L)}{\pi}$。最终,我们得到:
\[I = diffuse reflectance\]至此可以看出,将渲染方程中的余弦项移至BRDF评估函数后,该因子可与π项相互抵消,最终方程中仅保留反射率参数。这一数值在蒙特卡洛积分(如路径追踪)中具有实际意义,我们将其称为样本权重。当光线与表面相交并根据BRDF采样反射方向时,该光线”携带”的光照能量需通过此权重进行调整,以正确反映表面材质特性。
这种构建概率密度函数(PDF)与BRDF高度匹配的采样方法,不仅简化了代码实现,还能有效降低蒙特卡洛估计器的方差(噪声),因此是BRDF实现的重要考量因素。典型的应用案例是我们后续将讨论的可见法线分布(VNDF)采样方法。
3.2 Phong Reflection Model
另一个在过去常与Lambertian模型结合使用的经典反射模型是Phong模型,它提供了一个计算廉价的镜面高光实现方案。需注意区分Phong反射模型与Phong着色法——后者是通过法线插值实现高光平滑化的渲染技术。虽然Phong原论文声称其反射模型具有物理依据(基于真实材质的观察推导),但按现代物理渲染标准,它缺乏off-specular peek、菲涅尔效应等现象,无法视为真正的物理可信模型。其数学表达式为:
\[f_{Phong}(L, V)=specular\_reflectance(R\cdot V)^{shinese}\]对应的代码实现为:
1
brdfPhong = specular_reflectance * pow(dot(R, V), shinese) * dot(N, L);
可以发现,与Lambertian BRDF一样,在Phong模型的代码实现中我们添加了cosine项。
高光的宽度由指数(常称为光泽度或shine)控制,该参数理论上无界,但实际应用中通常将其取值范围限制在约10000以内。在计算Phong模型时,传统方法需要计算反射向量$R$,但Blinn在其优化版本中,使用了半程向量$H$以取代其计算。并且,Blinn在其优化版本中将Phong镜面高光与Lambertian漫反射及恒定环境光项结合,形成了Blinn-Phong反射模型。该模型曾长期作为实时渲染领域的标准方案,直至被更先进的基于物理的模型所取代。模型中现已过时的环境光项最初用于模拟间接光照,现已被基于图像的照明、实时光线追踪等技术替代。
3.3 Oren-Nayar Diffuse Reflectance Model
一种更先进的漫反射模型——Oren-Nayar模型[——通过引入表面粗糙度参数扩展了经典理论。该模型基于对粗糙表面的观测发现:当视线方向趋近于入射光方向时,实际反射光强会超过Lambertian模型的预测值(这种现象称为反向散射,月球表面就是典型的非Lambertian实例)。Oren-Nayar模型通过泛化Lambertian模型,使其响应表面粗糙度与观察方向的变化,从而有效捕捉此类光学现象。该模型的推导同样基于微表面理论框架,这与后续章节将讨论的基于物理的镜面反射模型具有理论基础的一致性。此模型特别适用于表现织物、石膏墙、沙石等具有微观结构特征的漫反射材质。
需注意,当该模型与镜面BRDF结合使用时,其底层微表面模型和分布函数可能不同(Oren-Nayar采用V型空腔模型和斜率的高斯分布),此时粗糙度参数可能需要在不同模型间进行转换或重映射至合理范围。由于Oren-Nayar模型中的粗糙度(记为σ)定义为微表面朝向角的标准差,因此其单位采用角度制。Lagarde在Frostbite引擎相关论文提出Beckmann粗糙度与Oren-Nayar粗糙度的转换关系为:
\[roughness_{OrenNayar}=\frac{1}{\sqrt 2}arctan(roughness_{Beckmann})\]本篇博客所使用的Oren-Nayar模型的数学表达式为:
\[f_{OrenNayar(L, V)}=\frac{diffuse\_reflectance}{\pi}(N \cdot L)(A + Bmax(0, cos(\phi_v-\phi_l))sin\alpha tan\beta)\]其中
\[A = 1.0 -0.5\frac{\sigma ^2}{\sigma^2+0.33} \\ B=0.45\frac{\sigma^2}{\sigma^2+0.09}\\ \alpha=max(\theta_l, \theta_v)\\ \beta=min(\theta_l, \theta_v)\]其中$\theta_l$和$\theta_v$表示法线与光线(及视线)向量之间的夹角,同时$\phi_l$和\(\theta_v\)表示这些向量在法线平面上的投影之间的方位角(即向量投影到法线平面后的夹角)。我们可以通过计算这些向量在法线平面上的投影来获取正确角度,但优化版本(通过引入平方根运算替代部分三角函数)可参考《Physically Based Rendering中的实现方案。
3.4 Disney(Burley) Diffuse Model
另一种广受欢迎且广泛应用的模型是Disney漫反射模型,有时也被称为Burley漫反射模型。这是一种基于实测数据观察得出的经验模型,其特点在于包含了与粗糙度相关的掠射角逆向反射现象。在此特性上,该模型与Oren-Nayar模型类似,但计算复杂度更低。该模型基于Schlick菲涅尔近似公式,通过扩展基础Lambertian模型,根据粗糙度参数在特定边界(0.5至2.5)内对掠射角反射率进行增强或衰减调整。其数学表达式为:
\[f_{Disney}(L, V)=\frac{diffuse\_reflectance}{\pi}(1+(F_{D90} - 1)(1 - cos\theta_l)^5)(1+(F_{D90}-1)(1-cos\theta_v)^5)\]其中:
\[F_{D90}=0.5+2*roughness*cos^2\theta_d\]由于该模型并非基于微表面理论推导(与Oren-Nayar模型不同),其粗糙度参数在微表面法线统计分布层面不具备相同物理含义,因此可能与镜面BRDF使用的粗糙度参数不兼容。Burley建议将粗糙度参数重映射至镜面BRDF粗糙度(α)的公式为:
\[\alpha=roughness^2\]此外,该模型不具备能量守恒特性,在注重能量守恒的渲染器(如路径追踪)中使用时可能存在问题。Lagarde在其关于寒霜引擎渲染技术的论文中描述了该模型的改进版本,显著提升了能量守恒性,并确保当与基于GGX的镜面BRDF结合使用时,反射能量始终不超过入射能量。
4 Microfacet Model
近年来众多BRDF模型均基于微表面理论构建。微表面模型的核心价值在于其能够更精确地表征粗糙表面的光反射行为——实验测量表明,这类表面的反射特性无法通过传统Lambert漫反射与菲涅尔反射的简单叠加准确描述。微表面理论的关键突破体现在其对离轴反射峰(off-specular peak)等复杂光学现象的解释能力,即当反射光强最大值偏离理想镜面反射方向时,该理论仍能有效建模此类非理想反射分布。
采用微表面模型的BRDF通常被称为”基于物理的”,意指其设计遵循物理(光学)定律而非单纯依赖经验观察。但在计算机图形学实践中,为实现计算可行性并提升实用性,我们常对理论模型进行简化近似处理,包括省略物理单位与参数。这种权衡使得物理原理与工程实践达成平衡:既保持光学理论基础,又满足实时渲染的算力约束,最终形成兼顾物理合理性与计算效率的实用型BRDF实现方案。
这类简化的典型范例是对菲涅尔方程中复杂折射率参数的省略处理(例如采用Schlick近似替代完整计算)。术语”物理合理(physically plausible)”常用于描述那些虽未严格遵循光学定律推导,但能模拟真实材质视觉特性的模型。实时渲染领域通常采用几何光学框架与RGB三元色表征光线,而非波动光学理论下的光谱分布分析。这种技术取舍使得渲染系统无法表现薄膜干涉引发的衍射效应及光的偏振现象,但换取了计算效率的大幅提升。
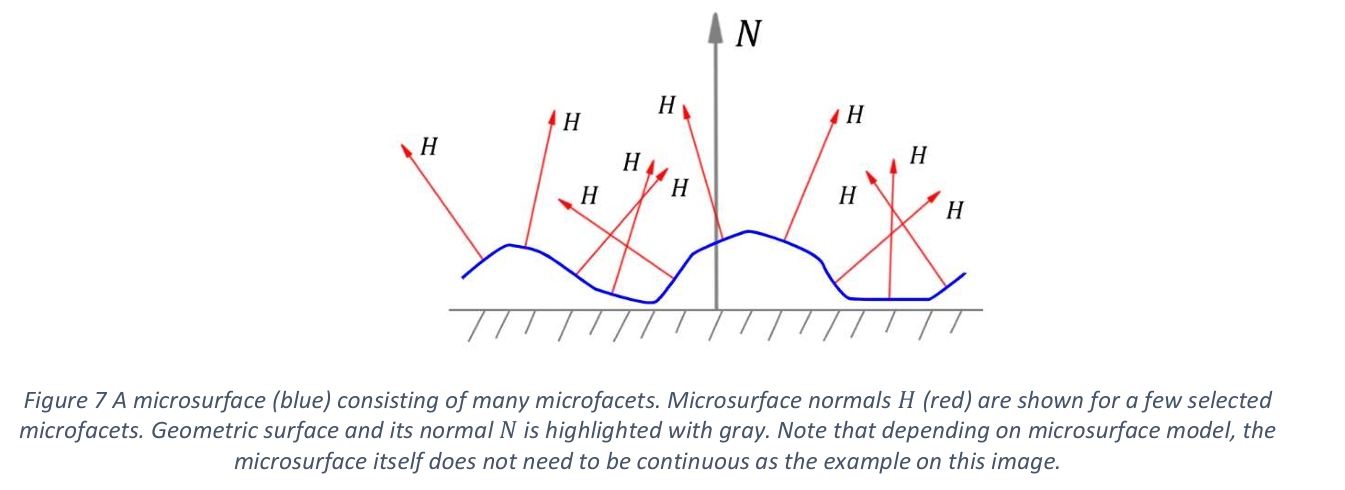
微表面理论将物体表面建模为由大量微表面组成的集合,这些微表面具有不同的坡度和高度(如下图所示)。微表面的变化程度和方式由微表面分布函数𝐷描述(通常依赖于粗糙度参数以控制表面外观)。这赋予BRDF特定的形状,从而影响材质的最终外观。
通常假设单个微表面表现为完美镜面反射,但也可以使用任意的BSDF(双向散射分布函数)。需要注意的是,该模型仅对几何表面进行建模,且微表面的效果通过微表面模型评估,因此我们只能观察到它们的聚合效应。
微表面模型的反射项定义为:
\[R = \frac{F(L, H)G(L, V, H)D(H)}{4(N\cdot L)(N\cdot V)}\]其中,$N$是法线,$H$是半角向量(指向光线方向$L$与视线方向$V$的中点方向)。该向量也被称为微表面法线、高光向量或半程向量,Blinn曾用它来优化Phong着色计算。所有这些术语将在后续章节详细讨论,此处仅作简要总结:
- D项(微表面分布函数)——告诉我们有多少比例的微表面朝向$H$方向,使得来自$L$方向的光线会被反射到$V$方向。
- F项(菲涅耳项)——评估在给定入射角下有多少光被表面反射。
- G项(几何衰减项)——计算微表面间相互遮挡(遮蔽与阴影),有时也用于BRDF的归一化。
- 分母——源自使用完美镜面作为微表面的模型推导。注意Cook和Torrance的原始论文在分母中使用常数π而非4,Walter指出这是由于𝐷项归一化方式不同,现代文献普遍采用常数4。
4.1 Distribution Term
NDF的本质是筛选满足“微表面法线 = 半角向量$H$”条件的微表面区域,可以用数学式进行表达:
\[D(H)=\frac{朝向H的微表面面积}{宏观表面总面积}\]需要注意的是,D项单独计算时忽略微表面间的遮蔽,遮蔽效应由G项单独处理。此外,此处的NDF不应与正态分布(即高斯分布)混淆,尽管它是NDF的一种可能实现方式。
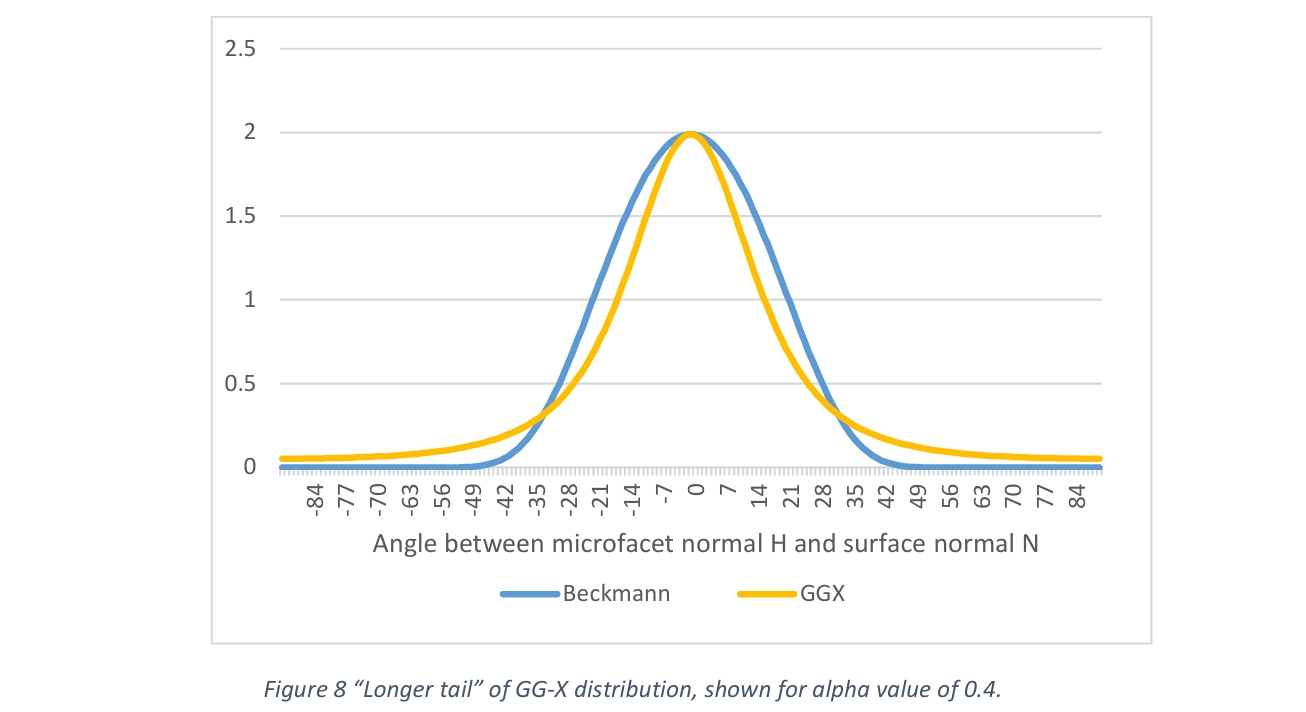
有多种不同的分布函数,例如Beckmann NDF,其使用直观的粗糙度参数(定义为微表面坡度的均方根斜率root mean square RMS)来控制其形状。另一个重要的NDF是GGX,与Beckmann相比,GG-X生成的镜面波瓣具有”更长尾部”,即高光峰值的衰减更缓慢(如下图所示),在掠射角处能够产生柔和的光晕。这更贴近许多实测的真实材质特性(例如金属边缘的辉光),因此GG-X被游戏行业广泛采用。此外,由于图形学界贡献的优化和近似方法,GG-X的计算通常更加高效。
Beckmann分布的数学表达式如下:
\[D_{Beckmann}=\frac{e^{\frac{-tan(\theta_h)}{\alpha^2}}}{\pi \alpha^2cos^4\theta_h}\]其中,$\theta_h$表示$N$与$H$之间的夹角,$\alpha$则表示粗糙度。$\alpha$与微表面均方根(RMS)斜率$\sigma$的关系为$\alpha = \sqrt{2\sigma}$。作为优化,我们可以使用Hoffman所介绍的等效公式$tan^2(\theta_h)=\frac{1-cos^2\theta_h}{cos^2\theta_h}$,也就是通过计算点积以避免正切函数的计算,这样的话,我们有:
\[D_{Beckmann}=\frac{e^{\frac{cos^2\theta_h-1}{\alpha^2cos^2\theta_h}}}{\pi \alpha^2cos^4\theta_h}\]GG-X分布的数学表达式如下:
\[D_{GGX}=\frac{\alpha^2}{\pi \big( (a^2-1)cos^2\theta_h+1 \big)^2}\]不同模型对粗糙度的定义单位可能截然不同。Torrance-Sparrow模型和Oren-Nayar模型直接使用正态分布的标准差,Beckmann和Trowbridge-Reitz模型使用微表面斜率的统计均方根(RMS),而Burley模型则采用经验选择的合理范围值。当多个BRDF耦合使用时(通常是高光BRDF和漫反射BRDF),必须谨慎地将美术师指定的粗糙度转换为底层BRDF所需的粗糙度单位。迪士尼的Principled BRDF提供了一个优秀的转换范例:他们将粗糙度参数重新映射为高光BRDF使用的𝛼值,即粗糙度的平方。这使得粗糙度的调整在感知上更线性,并与底层漫反射BRDF兼容,但需注意在计算𝐷和𝐺项时需再次对𝛼取平方(见前文公式)。另一种方案是为每个BRDF单独指定粗糙度参数以获得更多美术控制权。
4.2 Geometric Attenuation Term
几何衰减项𝐺用于量化因微表面几何结构导致的反射光衰减,即微表面间相互遮挡的影响。具体来说,包含两种相互遮蔽:
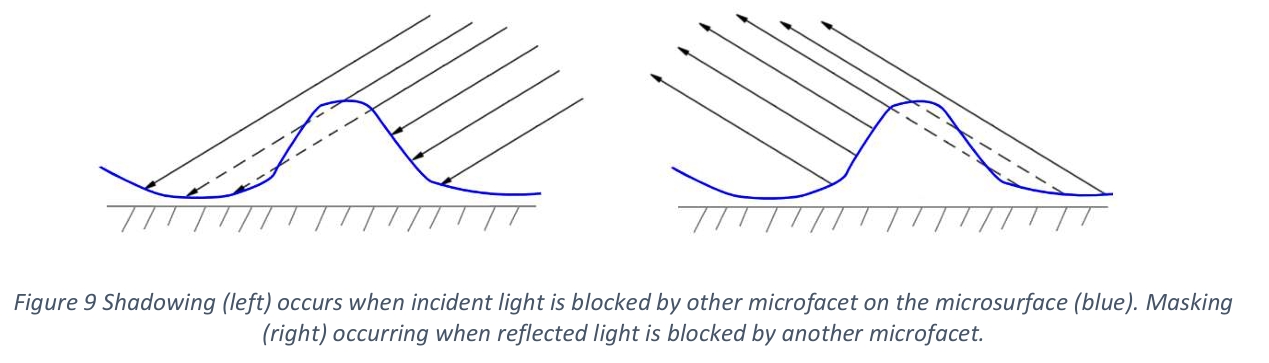
- 遮蔽(Masking):微表面凸起部分阻挡入射光(影响入射路径)
- 阴影(Shadowing):微表面凹陷部分阻挡反射光(影响出射路径)
G项有时也用于BRDF的归一化。如Torrance和Sparrow所指出的,𝐺项与菲涅耳项存在抵消效应,并导致特定粗糙度材质的”离轴高光峰值”现象——当菲涅耳项预测高反射率时,掠射角下𝐺项的显著阴影衰减使实际反射峰值出现在较小角度。
Smith几何衰减项是微表面模型中描述光线因微表面间相互遮挡(遮蔽与阴影)而衰减的核心函数。与早期的V-Cavity模型相比,Smith模型基于微表面斜率的统计分布,更符合真实物理规律,同时兼容任意法线分布(Beckmann、GGX等),并支持各项异性遮蔽计算,现已成为现代PBR(基于物理的渲染)的标准选择。
基于Smith模型的G项数学表达式如下:
\[\begin{align} G_1(H,S)=\frac{1}{1+\lambda(a)}\\ a=\frac{(H \cdot S)}{a\sqrt{1-(H\cdot S)^2}} \end{align}\]其中,$S$表示$L$或$V$二者之一,而$H$则是微表面法线,$\lambda$是与NDF相关的函数,如下所示:
\[\begin{align} \lambda_{GGX}(\alpha)=\frac{-1+\sqrt{1+\frac{1}{\alpha^2}}}{2}\\ \lambda_{Beckmann}(\alpha)= \begin{cases} \frac{1-1.259\alpha+0.396\alpha^2}{3.535\alpha+2.181\alpha^2}, \alpha<1.6 \\ 0, \alpha\geq1.6 \end{cases} \end{align}\]Walter提出的有理近似法旨在简化Smith模型中$\lambda$函数的计算,尤其是针对Beckmann分布,通过避免昂贵的误差函数计算,提升实时渲染效率。
几何衰减的产生是由于:虽然许多微表面可能朝向某个方向并反射特定入射角度的光线,但最终只有最靠近光源的微表面能实际反射光线(其他微表面会被shadowing)。同理,反射光线在离开微表面时也可能被其他微表面阻挡(称为遮蔽,masking)。Smith的𝐺函数可同时处理入射阴影𝐺(𝐻,𝐿)和出射遮蔽𝐺(𝐻,𝑉),二者的组合形成了完整的遮蔽-阴影函数,即:
\[G_2=G_1(H, L)*G_1(H, V)\]该组合公式假设遮蔽(masking)与阴影(shadowing)之间无相关性,但这并不准确,因为微表面中较深的微表面(如凹陷处)同时被阴影和遮蔽的概率更高。这一问题可以通过使用高度相关(height-correlated)形式的Smith遮蔽-阴影函数来解决:
\[G_2=\frac{1}{1+G_1(H, L)+G_1(H, V)}\]需要注意的是,无论是哪种形式的𝐺都可以用于之前介绍的微表面模型反射公式中的𝐺项,但高度相关版本更优,因为它仅略微增加计算量却显著提升精度。针对GGX分布的高度相关𝐺,Lagarde提出了一种高度优化的实现方案:通过将GGX分布的𝐺项代入公式并化简,得到的表达式中部分项会与微表面模型的分母相互抵消,从而进一步降低计算开销。Hammon提出了另一种有趣的高度相关𝐺近似方法(适用于GGX),其计算速度极快但会引入一定误差。对于Beckmann分布,我们的代码示例未提供此类优化,仍直接计算所有项。
由于𝐺项实际上指定了可见微表面的比例,NDF与𝐺的组合项(𝐷∗𝐺)给出了可见法线的分布,这是我们后续将要讨论的高效采样方法的基础。
需要注意的是,截至目前我们假设被阴影或遮蔽的光线会完全损失,但即便在我们假设微表面完全光滑的简化模型中,这也不符合实际情况。这正是基于微表面的BRDF发生能量损失的根本原因。遗憾的是,建模微表面间的多次散射非常复杂且计算代价高昂,实时渲染中通常将其忽略。
4.2.1 Anisotropic Materials
呈现各向异性反射的材质(如拉丝金属)可通过使用各向异性版本的法线分布函数(NDF)及其对应的几何项进行建模。关于该主题的深入讨论可参考Heitz和Ward的论文。这些函数的计算通常更复杂,且由双分量粗糙度值控制(两个垂直方向使用不同粗糙度)。计算必须在切空间(tangent space)中执行,以确保网格物体表面各向异性高光具有正确且一致的朝向。迪士尼原则化BRDF的相关文章展示了使用额外各向异性参数进行直观参数化的方法,该参数与标准粗糙度参数结合使用,在合理范围内计算二维粗糙度。
《基于物理的渲染》提出了一种更简化的解决方案:仍使用各向同性版本的法线分布函数(NDF)和几何项(𝐺),但根据各向异性高光应出现的方位调整粗糙度值。
4.3 Fresnel Term
菲涅耳项(Fresnel term)𝐹决定了有多少光会被表面反射,本质上告诉我们有多少光会贡献到当前计算的BRDF中。剩余部分(1−𝐹)将传递给底层材质(如漫反射BRDF或透射BTDF)。我们目前的实现仅讨论了两层材质(高光层与漫射层),但实际上可以创建包含多层的复杂材质。菲涅耳项需要在光线穿越各层介质的每个界面处进行计算。为简化模型,通常假设各层厚度为零,但若结合光谱渲染并赋予某些层厚度,则可模拟出当层间界面薄于光波长时发生的衍射现象(虹彩效应)。关于分层材质的深入探讨,建议参考Autodesk的文章[7]、Jakob等人的研究[47]以及Weidlich和Wilkie的著作[48]。虹彩效果的具体实现可参阅Belcour与Parla的最新论文[49]。
菲涅耳项的取值取决于视线方向与表面法线的夹角、材质属性(折射率和消光系数),由相对复杂的菲涅耳方程描述(该方程还涉及光的偏振特性)。无论何种材质,菲涅耳项在掠射角(grazing angles)时总会趋近于1,即所有光线均被反射,但在中间角度范围内会发生Cook与Torrance提出的”颜色偏移”现象[30]。
Schlick提出了广泛使用的菲涅耳项近似方法。他指出,完整的菲涅耳方程不仅计算成本高昂,还依赖于难以直观理解的折射率𝑛和消光系数𝑘,这不符合我们对可预测且易用参数的需求。更复杂的是,完整的折射率是一个包含实部(折射率)和虚部(消光系数)的复数,且需按波长指定参数,这在使用RGB三元组进行渲染时并不适用。
Schlick的近似方法基于这样一个观察现象:当以90度视角观察时,所有材质均呈现完美反射率。我们只需使用单一参数——表面在正入射(0度)时的反射率(𝐹₀),即可近似完整的菲涅耳方程:
\[F=F_0+(F_{90}-F_0)*(1-\,u^5)\]其中,$\mu$表示观察方向与法线夹角的余弦值,而$F_{90}$在默认情况下为$1$。需注意,此公式已消除折射率和消光系数的影响,但需额外指定正入射反射率$F_0$。使用Schlick公式的另一后果是着色计算无法考虑光的偏振特性。
4.3.1 Specifying Reflectance at Normal Incidence
消除折射率𝑛和消光系数𝑘虽然简化了计算,但也导致无法直接控制材质表现为绝缘体或导电体。这两类材质的核心差异在于:金属的反射会带有base color染色(因部分光谱被吸收),而介电质的反射则保持光源颜色不变。如Cook与Torrance所述,金属在正入射时的反射颜色由材质base color决定(记作$F_0$)。基于这一认知,我们可通过引入”金属度(metalness)”参数来”修正”金属的菲涅耳反射颜色,该参数将𝐹混合介电质默认反射率与金属基色:
\[F_0=lerp(F_{0Dielectrics}, baseColor, metalness)\]通常选择$F_0$为$0.04$吗,也就是4%的反射率,例如UE4和Frostbite均采用此值。需要注意的是,某些现实材质(如水)的反射率更低(0.02),而部分介电质材料(如钻石)的反射率更高(0.18)。该值在渲染器中固定不变,并不随材质改变,但其选择对最终视觉效果影响重大。金属度参数还会衰减金属材质的漫反射,该衰减基于base color进行计算:
\[diffuse\_reflectance=base\_color *(1-metalness)\]这种参数组合(basecolor与金属度)常被称为金属度工作流(metalness workflow),其局限性在于无法为漫反射和镜面反射设置不同色调。另一种方法是镜面反射工作流(specular workflow)[54],该方法允许直接指定漫反射和镜面反射率,而非通过基色计算。此方法需要更多存储空间,但通过允许漫反射与镜面反射差异显著(甚至包含非真实材质),提供了更大的艺术自由度。
对于某些材质,可能需要更精细地控制从$F_0$到1的过渡过程,以减少Schlick近似的误差。虽然$F_0$的RGB值通常基于正入射测量或计算得出,但某些材质(如特定金属和涂层表面)在中间角度可能出现轻微色偏,或是创作非真实材质(如幻彩金属)时需特殊处理。Gulbrandsen通过引入两个参数(基础反射率和边缘色调)解决该问题。Hoffman近期提出了改进方案[,新增参数$h$控制边缘衰减,并整合Lazanyi误差修正项来降低Schlick近似误差。参数$h$可理解为82度入射角时的反射率$F_{82}$,可通过物理精确计算或实测获得。
需注意,$F_0$原本依赖于表面两侧介质的折射率,而我们通常假设材质被空气包围。若非如此(如在水下),应相应调整$F_0$。 Lagarde提出了一种有趣的菲涅耳项优化方案,采用球面高斯近似(Spherical Gaussian approximation),也就是通过指数形式以避免幂函数计算,该方案已被应用于UE4:
\[F=F_0+(F_{90}-F_0)*2^{-5.55473*\mu-6.983146*\,u}\]关键的实现细节在于:菲涅耳项必须基于采样微表面的法线(半角向量)而非宏观表面法线(或着色法线)进行评估。否则材质的粗糙度对菲涅耳项的影响将被忽略,导致物体反射表现比实际更强烈。
4.4 Sampling the Microfacet BRDF
[略]
5 Combining BRDFs
要将镜面BRDF与漫反射BRDF结合,我们采用基于菲涅耳项的简单混合方法:镜面反射部分由菲涅耳项$F$加权,漫反射部分由$(1-F)$加权。这种方法的灵感来源于分层材质理论——光线与表面各层相互作用,菲涅耳项决定多少光反射(贡献镜面波瓣),多少光透射进入次层(贡献漫反射波瓣)。通过此方法,任意BRDF都可分层组合,例如业界广泛采用的GGX微表面镜面BRDF与Lambert/迪士尼漫反射BRDF的结合。更复杂的多层材质通常包含1-2个镜面波瓣(模拟透明涂层)、带次表面散射的漫反射BRDF以及透射BTDF。需注意:每层BRDF自身必须满足能量守恒。
需要注意的是,计算漫反射BRDF层时需已知镜面BRDF层的菲涅耳项$F$。在代码中,我们为镜面BRDF采样半角向量并用于菲涅耳项计算,即使仅评估漫反射项。这种操作计算成本较高,可采用近似归一化项或预计算查表法优化。
更精确但更复杂的解决方案是使用专为协同工作设计的漫反射-镜面组合模型。另一种方案是选择主BRDF并匹配合适的漫反射BRDF直接叠加。实践中多层材质的更多案例可参考《使命召唤》材质系统解析。
组合多个BRDF时,最终结果仍需满足能量守恒和亥姆霍兹互易性(Helmholtz reciprocity)原则,但在实际应用中往往难以完全实现。
5.1 Energy Conservation
BRDF必须遵守的基本原则之一,是能量守恒要求——表面反射的光线不应超过入射光量。此外,若表面是完美反射体(白色反照率),也不应发生能量损失。然而在实际中,即使是基于物理的微表面模型BRDF,仍常出现能量损失,其主要原因是微表面之间缺乏多次反射。
在构建实时渲染的材质模型时,能量守恒问题过去常被忽视,尤其是仅使用单次反射光照时。对于路径光线追踪和全局光照算法,必须确保光线从表面反弹时不会额外产生能量,否则路径追踪器的收敛性将无法保证。一种易于实现且实用的能量守恒测试是白炉测试,即在全方位白色光照下渲染一个白色球体。若材质遵守能量守恒,球体应完全融入白色背景中,如下图所示(图中有两个白球)。任何差异均表明存在能量损失或增益。由于球体渲染覆盖了所有可能的视线与光线向量组合,我们能清晰观察到能量异常发生的角度范围。
6 Parameterizing the BRDF
本章节将总结所述BRDF参数与美术人员设置的材质属性之间的关联。截至目前,我们已使用以下参数:
- Specular BRDF
- Specular Reflectance at normal incidence, 记作$F_0$
- Roughness
- Diffuse BRDF
- Diffuse Reflectance
- Roughness
我们不直接使用Diffuse/Specular Reflectance,而是通过base color与metalness计算它们,从而避免创建出物理上不可能的材质,并支持电介质与金属的区分建模。粗糙度值直接指定,并按照迪士尼原则化BRDF的方式(平方处理)重映射至镜面BRDF。