LTC Area Light from Heitz's Paper
1 Introduction
基于物理的着色的核心在于求解光照方程,即对BRDF与场景光照在半球空间上的乘积进行积分。而本篇博客主要关注多边形光源的着色计算,这意味着需要对球面多边形区域上的BRDF进行积分。这里的球面多边形(spherical polygon)区域表示三维空间的多边形光源投影到着色点法线方向上的半球所形成的区域。
尽管多边形光源在理论上是最简单的光照模型之一,但其在实时渲染中存在两大挑战:
- 积分难以计算:对spherical polygon进行参数化spherical分布的积分通常非常困难,即使是最简单的分布也不例外。例如,Phong-polygon积分的解析计算成本极高,而球面高斯函数则不存在解析解。
- BRDF模型的分布复杂:最先进的基于物理的材质模型并非简单分布;它们具有复杂的形态,包含各向异性拉伸(stretching)与偏斜(skewness)特性,需精确表征才能实现材质的真实感。
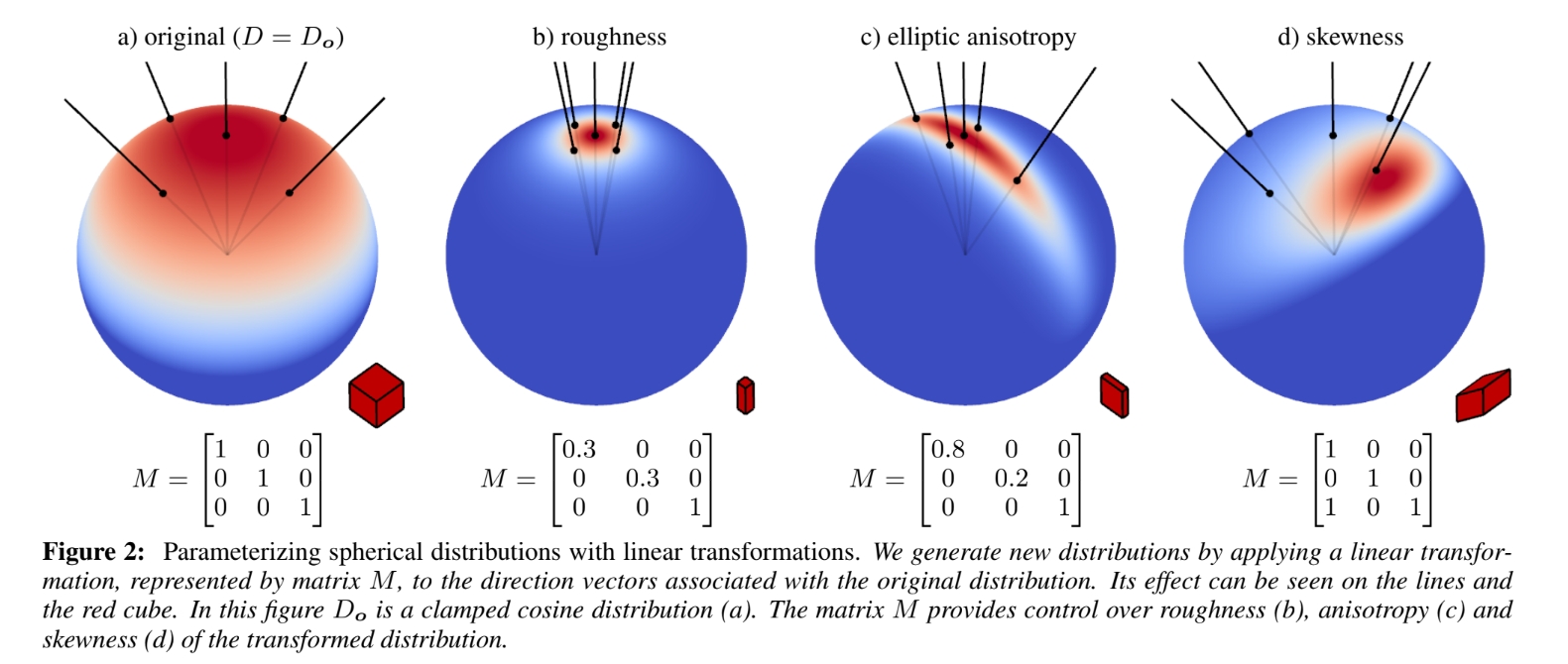
在本篇博客的第三章节,我们提出了线性变换球面分布(LTSDs),这是一种新型spherical分布,可解决上述两个问题。我们从原始spherical分布出发,对其方向向量施加由3×3矩阵表示的线性变换。这产生了一种参数化方法,使我们能够调整原始分布的形态,例如粗糙度、椭圆各向异性和偏斜度(如下图所示)。
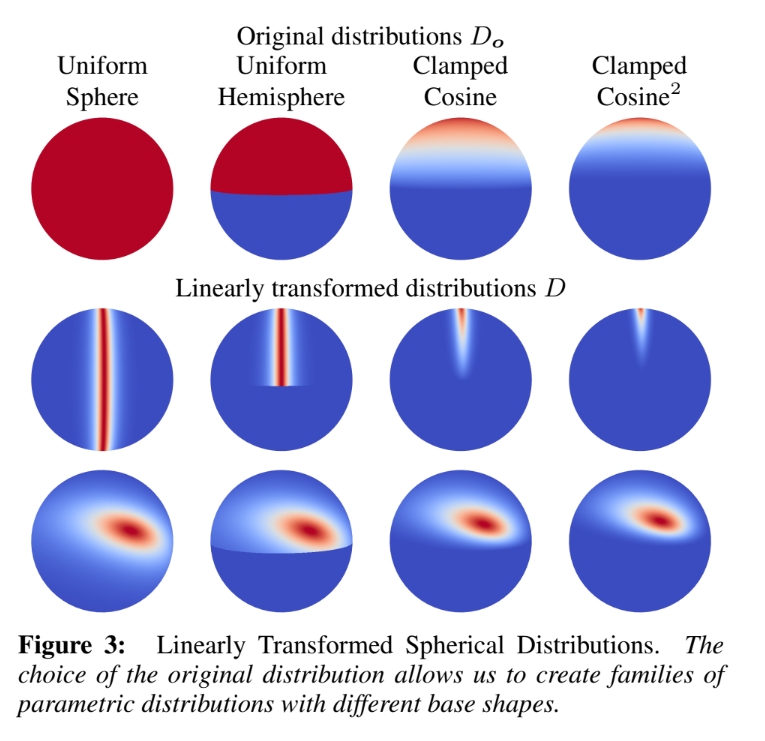
借助该参数化机制,我们可利用任意spherical分布创建具有不同基础形态的参数化分布族(如下图所示)。这类分布的核心特性在于继承了原始分布的归一化、任意球面多边形积分及重要性采样等关键属性。
在第四章节中,我们证明:当原始分布采用截断余弦分布时,将生成一类新分布——称为线性变换余弦(LTCs)——由于其覆盖的球面形态多样性,可良好地近似基于物理的BRDF。此外,由于截断余弦分布可在任意球面多边形上解析积分,LTCs同样具备此特性。在第五章节中,我们展示了如何在实时多边形光源着色应用中利用该特性。
2 Previous Work
2.1 Polygonal-Light Shading
目前针对多边形光源的解析解仅限于类余弦分布。对多边形区域进行截断余弦积分(即计算多边形irradiance)的方法由Lambert于两个世纪前提出,并由Baum等人引入计算机图形学。Arvo[将其扩展至Phong分布(即通过指数控制锐度的余弦分布),Snyder提供了该技术的具体实现。此方法的主要局限在于Phong-多边形积分的复杂度为$O(e\cdot n)$,即计算成本随分布锐度增加。因此游戏常采用近似方案,如最具代表性点启发式(用点光源代替面光源)。这类方法虽满足实时性,但存在精度缺陷:结果可能出现数量级偏差与视觉瑕疵。Lecocq等的最新研究提出$O(n)$复杂度的Phong-多边形近似积分方案,但其仍受限于Phong波瓣的旋转对称性。他们将Phong分布作为微表面分布积分于非多边形半空间域,通过多边形近似域实施积分。虽然恢复了微表面模型各向异性,但多重近似仍导致视觉瑕疵。相比之下,我们的技术虽同为O$O(n)$复杂度,却能实现精确积分,且支持椭圆各向异性和偏斜形态。我们的技术实现更为简单:只需将多边形顶点乘以矩阵后应用经典Lambert公式计算irradiance即可。
2.2 Spherical Distributions
现有球面分布中,既能表征复杂形态又具备实用积分特性的方案极少。球谐函数仅适用于低频形态。计算机图形学中最常用的全频段分布为旋转对称型波瓣:Phong分布或球面高斯分布。尽管结构简单,其积分已然是难题。如上所述,Phong分布在球面多边形上的高效积分需依赖近似;类似地,球面高斯分布在锐利球面域上的积分也只能近似求解并依赖预计算查找表。此外,设计更复杂的分布往往意味着牺牲简洁特性。因此,推导其在球面多边形积分的实用解法几无可能。
3 Linearly Transformed Spherical Distributions
在本章节中,我们介绍线性变换球面分布(LTSDs)。我们将展示如何通过对原始分布的方向向量施加线性变换来重塑其形态,定义由此获得的新分布,并讨论其特性。
3.1 Definition
Original Distribution to be Transformed
$D_o$表示我们通过线性变换进行重参数化的基础分布。$D_o$的选择决定了变换后分布的基础形态。
Linear Transformations
要生成新分布$D$,我们向原始分布$D_o$的方向向量$\omega_o$施加由3×3矩阵$M$表示的线性变换。需注意:本文始终假设方向向量已归一化。
Closed-Form Expression
线性变换球面分布(LTSD)的强度等于原始分布$D_o$在原始方向$\omega_o$处的强度,乘以由球面变换畸变引起的立体角度量变化。