The Visibility Problem the Depth Buffer Algorithm and Depth Interpolation

当像素与三角形重叠时，我们将其视为与三角形表面上一点重叠。当然，一个像素可能会有多个点重叠，此时我们的解决办法是比较与像素重叠的每一个点的深度值，找出距离相机最近的点。这样，我们就可以引出depth buffer这个概念了。它是一个与frame buffer尺寸相同的二维浮点数数组，它用于在光栅化过程中记录物体的深度值。

---

Finding Z by Interpolation

depth buffer的定义和使用方法都比较好理解，所以我们现在的问题是如何计算深度值。我们首先再次明确一下深度值的含义。当一个像素与三角形重叠时，它会覆盖三角形上的一个微小表面，为了简化，我们将该微小表面视为单个点，我们的目标就是计算该点的Z坐标。

在投影阶段，我们将栅格空间空间中的投影点声明为一个三维点，其中Z坐标就是三角形顶点在相机空间中的Z坐标的负值，即：

\[P_{\text{raster}}.z=-P_{\text{camera}}.z\]

既然已知了投影三角形的三个顶点的Z坐标，我们只需要根据重心坐标插值即可：

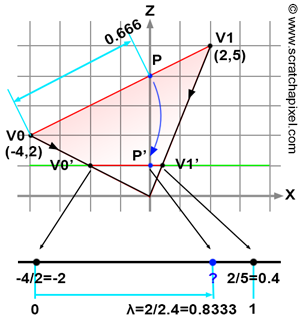
\[P.z = \lambda_0 \cdot V0.z + \lambda_1 \cdot V1.z + \lambda_2 \cdot V2.z.\]

但实际上这种方法是错误的。通过重心坐标插值计算的前提是，对应的属性在三角形表面上是线性变化的，而当三角形经过透视除法被投影到canvas上，Z值就不再在2D的三角形表面上线性变化了。换种说法的话，透视投影保留了直线但不保留距离，三维空间中物体的距离比例无法在投影到2D平面时保留。如下图所示：

那我们应该如何计算深度值呢？答案是使用深度值的倒数进行插值，也就是：

\[\dfrac{1}{P.z} = \dfrac{1}{V0.z} \cdot \lambda_0 + \dfrac{1}{V1.z} \cdot \lambda_1 + \dfrac{1}{V2.z} \cdot \lambda_2.\]