Overview of Coordinates Transformations in Rasterization

本篇博客以这篇博客为基础

在计算机图形学中，变换实际上是对物体的顶点所在的坐标系进行操作，而不是直接操作物体本身。

From Local Space to World Space

这部分没什么好说的，将物体从其局部坐标系（物体自身的坐标系）变换到世界坐标系中。这涉及对物体进行平移、旋转和缩放。

---

From World Space to Camera Space

当我们平行或旋转相机时，我们实际上是在变换相机的局部坐标系。在计算机图形学中，这个局部坐标系又被称为相机坐标系，它定义了相机的位置与朝向，从而决定了渲染场景的视角。

相机本质上是一个坐标系，那么物体顶点可以从模型空间变换到世界空间，也就可以从世界空间坐标系变换到相机坐标系中。但是，我们需要思考，为什么要变换到相机空间呢？

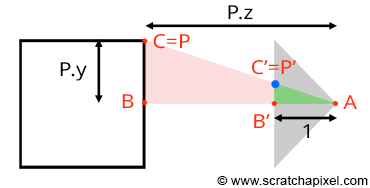
在光栅化算法中，我们想要计算点$P$在图像平面上的投影点$P’$的坐标。如图所示，连接眼睛（即相机空间的原点）与点$P$，所构成的线段与image plane的交点即为$P’$。如果我们能够在相机空间中定义出点$P$的坐标，则我们可以根据相似三角形定理轻松地计算出投影点$P’$的坐标值。具体来说，我们可以构建出两个相似的三角形，即$\triangle ABC$与三角形$\triangle A’B’C’$，其中：

• $A$：相机空间原点
• $B$：相机与点$P$在相机空间Z轴上的距离
• $C$：相机与点$P$在相机空间Y轴上的距离
• $B’$：相机与image plane的距离，实际上就是相机的焦距。为了便于计算，我们假定距离为$1$
• $C’$：相机与投影点$P’$在相机空间Y轴上的距离

根据相似三角形的性质，我们可得：

\[\frac{BC}{AB} = \frac{B'C'}{AB'}\]

我们已知边$AB’$为$1$，并且已知$B$与$C$的值，分别为点P在相机空间中的Z坐标与Y坐标。代入等式，得：

\[\displaylines{\frac{P.y}{P.z}=\frac{P'.y}{1}\\ P'.y=\frac{P.y}{P.z}}\]

这个公式在计算机图形学中相当重要，也就是我们所说的透视除法。我们可以将同样的推导应用在X坐标上，即投影点$P’$的X坐标值为：

\[P'.x = { P.x \over P.z }\]

我们需要在这里强调，透视除法成立的前提是，点处于相机空间中，但我们将模型导入场景时，默认顶点都处于模型空间，所以我们需要首先进行空间变换。所以，我们不妨再清晰地表述一下上面的式子：

\[\displaylines{P'.x = \dfrac{P_{camera}.x}{P_{camera}.z}\\ P'.y = \dfrac{P_{camera}.y}{P_{camera}.z}}\]

但是，在实践中，我们通常保持坐标转换过程中的一致性。如果一个点在世界坐标系中位于y轴的左侧，那么在相机坐标系中，它也应该位于y轴的左侧。同样地，如果世界坐标系的x轴指向右，那么相机坐标系的x轴也应该指向右。为了实现这种一致性，最简单的办法就是让相机指向-Z轴的方向。这样，当一个点从世界坐标系转换到相机坐标系时，x轴和y轴的方向保持一致，确保点的位置正确转换。

相机始终指向相机坐标系的-Z方向，那从世界空间变换到相机空间的过程中，是否需要额外反转Z轴的坐标呢？单从技术的角度来说，这样是合理的，只是按照惯例，我们通常不需要明确地反转相机的Z轴，使用普通的变换矩阵即可。当我们创建一个相机时，相机默认朝向-Z方向，但如果我们检查相机的矩阵，会得到一个单位矩阵，表明并没有应用任何反转。

我们可以考虑这样一个例子。假设一点的坐标为(0, 0, -10)，且相机的坐标为(1, 0, 2)。则相机的矩阵为：

\[\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 2 & 1 \end{pmatrix}\]

我们对该点应用这个相机矩阵，就可以得到该点相对于相机的坐标，也就是该点在相机空间中的坐标，为(1, 0, -12)。可以看到，变换到相机空间中的点是负的，表明相机依然是朝向-Z方向。此时，我们对该点执行透视除法，那么该点的X坐标$P’.x$为$\frac{1}{-12}$，是一个负值，表明该点在相机视线方向的左侧，然而在变换前，该点在相机视线方向的右侧。

这个例子表明，如果我们忽略相机指向-Z方向，直接进行正常的矩阵变换，则会导致生成镜像的投影点坐标。

在渲染中，我们只会渲染相机前面的物体，而丢弃相机后面的物体，所以顶点在相机空间的Z坐标一定是负数，所以在透视除法中，我们需要取顶点在相机空间中Z值的负数，即：

\[\displaylines{P'.x = \dfrac{P_{camera}.x}{-P_{camera}.z}\\ P'.y = \dfrac{P_{camera}.y}{-P_{camera}.z}}\]

---

From Screen Space to Raster Space

当顶点被投影到二维平面上时，投影点就变成了二维的点，此时，我们说投影点位于屏幕坐标空间上。

如果一个投影点的X坐标的绝对值超过了画布宽度的一半，或Y坐标的绝对值大于画布高度的一半，都会导致该投影点被裁剪，从而最终在图像中不可见。我们可以用下面这个式子来表述：

\[\displaylines{\text {visible} = \begin{cases} yes & |P'.x| \le {W \over 2} \text{ and } |P'.y| \le {H \over 2}\\ no & \text{otherwise} \end{cases}}\]

如果投影点是可见的，则该投影点最终会作为一个像素显示在图像中。像素与投影点一样，但不同的是，处于屏幕坐标空间中的投影点的坐标值是浮点数，而像素坐标值是整数，并且像素所在坐标空间是以图像的左上角为原点，X轴指向右方，Y轴指向下方。我们将像素所处的坐标系称为栅格空间raster space，像素在该坐标系下是一个单位大小的正方形。我们将由投影点变换到像素的过程称为screen space到raster space。那具体是怎么实现的呢？

首先我们要做的是将投影点坐标映射到$[0, 1]$的范围上，这一步很简单，因为画布的宽高是已知的，我们可以通过下面这个式子完成映射：

\[\displaylines{\begin{array}{l} P'_{normalized}.x = \dfrac{P'.x + \text{width} / 2}{\text{width}}\\ P'_{normalized}.y = \dfrac{P'.y + \text{height} / 2}{\text{height}} \end{array}}\]

重映射后的投影点位于NDC空间下。NDC空间中，坐标系原点位于画布的左下角，此时投影点的坐标依然是浮点数，只不过范围被映射到了$[0, 1]$上。

从NDC空间变换到栅格空间就很简单了，我们只需要将NDC坐标乘以实际的图像像素宽度与高度即可，也就是将X坐标的范围从$[0, 1]$映射到$[0, Pixel\;Width]$，将Y坐标的范围从$[0, 1]$映射到$[0, Pixel:Height]$。此外，由于栅格空间中，像素的坐标是整数，在映射结束后，我们还需要将坐标值向下取整。最后还有一个小细节，在NDC空间中，原点位于左下角，Y轴指向上方，而栅格空间中，原点位于左上角，Y轴指向下面，所以我们可以在映射之前完成Y轴的翻转。整个变换的过程用公式表达如下：

\[\displaylines{\begin{array}{l} P'_{raster}.x = \lfloor{ P'_{normalized}.x \times \text{ Pixel Width} }\rfloor\\ P'_{raster}.y = \lfloor{ (1 - P'_{normalized}.y) \times \text{Pixel Height} }\rfloor \end{array}}\]

在OpenGL中，从NDC空间变换到栅格空间的过程被称为视口变换。

---

Source Code

下面这个函数会将坐标从世界空间变换到栅格空间，也就是二维像素的坐标值。同时，如果该点在图像中不可见，函数会返回false：

bool computePixelCoordinates(
    const Point3f& pWorld, const Matrix44f& worldToCamera,
    const float& canvasWidth, const float& canvasHeight,
    const int& imageWidth, const int& imageHeight,
    Point2i& pRaster)
{
    Point3f pCamera;
    worldToCamera.multVecMatrix(pWorld, pCamera);

    Point2f pScreen;
    pScreen.x = pCamera.x / -pCamera.z;
    pScreen.y = pCamera.y / -pCamera.z;
    if (std::abs(pScreen.x) > canvasWidth || std::abs(pScreen.y) > canvasHeight)
        return false;

    Point2f pNDC;
    pNDC.x = (pScreen.x + canvasWidth / 2) / canvasWidth;
    pNDC.y = (pScreen.y + canvasHeight / 2) / canvasHeight;

    pRaster.x = static_cast<int>(std::floor(pNDC.x * static_cast<float>(imageWidth)));
    pRaster.y = static_cast<int>(std::floor((1 - pNDC.y) * static_cast<float>(imageHeight)));

    return true;
}