The Pinhole Camera Model

发表于 2024/08/03

作者 褴褛飞旋

22 分钟阅读

在上一篇博客中，我们大致了解了三角形顶点从世界空间变换到像素坐标的过程。这一篇博客是更进一步的拓展，我们将会研究基于物理的针孔相机模型在顶点坐标变换中的影响。

我们先来看看针孔相机的原理。

How a Pinhole Camera Works

在相机中，胶片的尺寸与光圈到image plane的距离对相机的成像有着至关重要的作用。在本篇博客中，我们将会讨论这两个因素对于图像质量的影响，并且会整合到我们的虚拟相机模型中。

Focal Length, Angle of View, and Filed of View

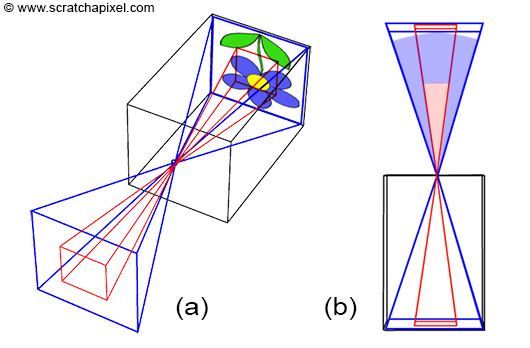
在相机模型中，我们将场景投影图像所在的平面称为image plane，当image plane靠近光圈时，物体会变得更小，场景中有更多的部分会被投影，我们用属于Zooming Out来描述这个过程。相反地，当image plane远离光圈时，场景中被投影的部分会变少，我们称之为Zooming In。我们可以用两种方式分别量化这个过程：

调整焦距，也就是image plane与光圈之间的距离。
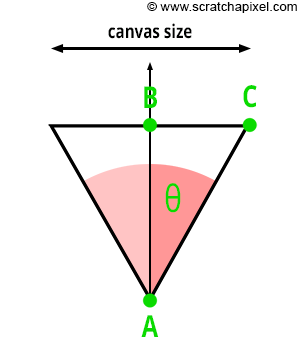
调整FOV，也就是由光圈和胶片两侧边缘定义的三角形的角度。FOV有水平和竖直之分。
- 不同的程序或API所使用FOV也不同，如OpenGL使用的是竖直FOV，而Maya使用的是水平FOV

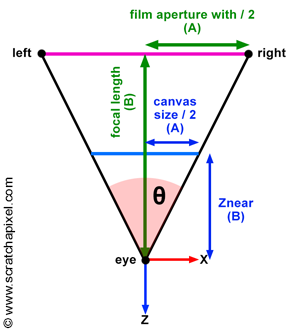
此外，如上图所示，我们可以看到，焦距与FOV之间有着直接的联系：当canvas尺寸固定时，焦距越大，FOV越小。

Film Size Matters Too

如上图所示，我们所捕获的场景的范围也会受到传感器尺寸的影响。传感器的尺寸越大，所捕获的场景的范围就越大。因此，胶片的尺寸与相机的FOV之前也存在着一定的关系：尺寸越小，FOV就越小。

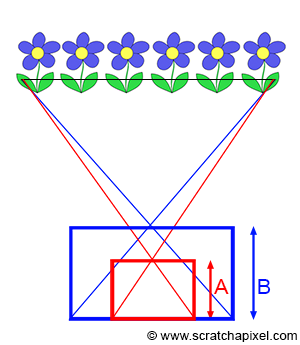
需要注意的是，有时我们可能会误解胶片尺寸与图像质量这二者的联系。当然，二者是有关联的，胶片的尺寸越大，理论上就能记录更多的细节，图像的质量就越高。但是，如果我们想要使用不同尺寸的胶片来拍摄相同的场景图片，就需要对应的调整焦距的大小，如下图所示中的A和B，分别代表了不同尺寸的胶片所使用的焦距：

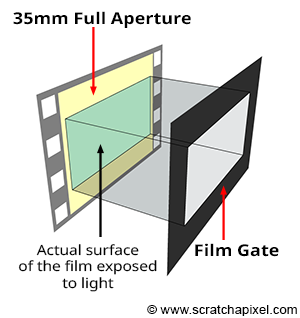
Film Gate这个术语指的是胶片前的矩形开口，它是可以自由调整的，从而可以允许我们修改胶片的格式。当然，对于数码相机来说，film gate通常表示的是胶片的宽高比。下图展示了film gate的作用机制：

此外，还有一个与film gate类似的概念，称为film back，它是相机中的一个结构，用于支撑和固定胶片。在Maya中，镜头相关的参数就被整合进了Film Back这个类中。改变Film Gate参数，就可以修改胶片的预设格式，进而改变Camera Aperture这个参数，该参数分别定义了胶片的宽和高。而参数Film Aspect Ratio则定义了胶片的宽高比。

这个地方我很想吐槽，原谅我水平有限，但是为什么胶片的参数要命名为Camera Aperture，这个参数不是只光圈吗？？？

现在，我们已经介绍了相机的焦距、FOV与胶片尺寸，我们需要明白：焦距和胶片尺寸是真实相机中我们可以调节的参数，而FOV是根据焦距和叫胶片尺寸计算而来。想要模拟真实的物理相机模型，我们需要考虑的就是焦距和胶片尺寸这两个参数。

Image Resolution and Frame Aspect Ratio

胶片的尺寸通常以英寸或毫米为单位，我们不应该将胶片的尺寸和图像的像素数量混淆。我们可以这样理解，胶片的尺寸会影响FOV，但是图像的分辨率却不会。这两个参数是完全无关的。

在数码相机中，传感器取代了胶片，我们可以将传感器的尺寸理解为等同于胶片的尺寸，但与胶片相比，传感器还多了一个属性，也就是包含的像素数量。下图是一个徕卡数码相机的传感器，它的尺寸为36mm x 24mm，分辨率是6000 x 4000，以像素为单位：

虽然说传感器自身包含了像素，但需要注意的是，像素数量仍然与FOV无关，像素分辨率仅仅会影响图片的清晰度。

而在CG中，这个理念是类似的，宽高比相同，但分辨率不同的若干图片可以描绘同一个场景，更高的分辨率可以提供更多的细节。我们可以将图像也类比为gate这样一个概念，称为resolution gate。我们会在稍微讨论resolution gate与film gate的区别以及二者之间的联系。

现在，我们可以定义出image/device aspect ratio这个概念了，它通过图像的分辨率计算而来。常见的宽高比有4：3、16：9、21：9等。

Canvas Size and Image Resolution: Mind the Aspect Ratio!

与胶片相机相比，数码相机有一个独有的特性，那就是传感器（或者说canvas，也就是绘制了三维场景的二位表面）的宽高比和图片的宽高比可以不一致。你可能会好奇，为什么要有这样的设定？

实际上，这种情况比预期中更常见。比如说，胶片帧（也就是胶片所记录的单帧静态图片）在扫描时所用的门（代表了一种宽高比）很可能与拍摄时用的门不同，这样自然会导致宽高比的不一致。这种情况在处理变形格式（如宽银幕电影）时也会出现。

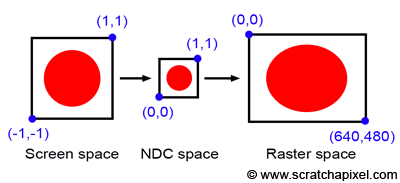
在我们深入了解变形格式anamorphic之前，我们先来考虑一下这种不一致性在光栅化中的情况。假设我们有一个正方形的canvas，它的两个极值点的坐标分别是(-1, -1)和(1, 1) ，并且上面有一个圆形的图像，如下图所示：

在光栅化算法中，从屏幕空间变换到NDC空间，需要将范围映射到[0, 1]上，但因为canvas本身就是正方形的，所以宽高比得以保留，图像也不会在某个方向上被拉伸或压缩。然而，如果最终图像的分辨率是640 x 480，在映射到栅格空间的过程中，宽高比会被映射为4：3，导致我们的圆球被拉伸了。我们可以得出这样一个结论：如果栅格图像的宽高比与canvas的宽高比不一致，将会导致图片失真。

你可能回想，为什么这种差异会发生。但实际上，这种失真的情况只是我们的推理与假设，在我们最终的相机模型中，canvas宽高比会由图像的宽高比计算而来。例如，如果图像的分辨率设置为640 x 480，那么canvas宽高比就会设置为4：3。

但如果，根据胶片尺寸film size（Maya中称为Film Aperture？？？不理解，尊重祝福）计算canvas宽高比，而非图片分辨率的话，则以不同纵横比的分辨率渲染图像可能会导致不匹配。例如，35 毫米胶片格式（学院尺寸）的尺寸为 22 毫米 x 16 毫米，长宽比为 1.375。然而，对完整 35 毫米胶片帧进行标准 2K 扫描会产生 1.31 的设备纵横比，从而导致画布和设备纵横比不同。

为了解决这个问题，DCC、游戏引擎等软件会提供将canvas宽高比与图像宽高比（或称设备宽高比）对齐的策略：

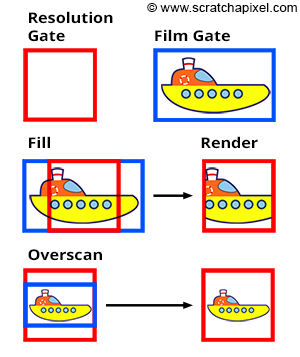
Fill模式会强制resolution gate置于film gate内
Overscan模式会强制film gate置于resolution gate内

两种模式的对比如下图所示：

Conclusion and Summary

如果我们想要模拟真实相机，我们需要根据焦距与胶片尺寸来计算FOV。

Implementing a Virtual Pinhole Camera

我们会在代码中构建一个虚拟针孔相机模型，它具备以下参数：

核心参数，需要我们自行为相机设定：

焦距 Type: float
- 相机与胶片/传感器的距离
- 可以说，焦距的用途非常单一，仅仅用于计算FOV
- 单位是毫米mm
胶片尺寸 Type: 2 floats
- 与焦距共同计算出相机FOV。
- 定义了相机film gate宽高比
- 通常以英尺inch为单位，不过我选择用mm
裁截面 Type: 2 floats
- 远近裁截面是一组与相机Z轴垂直，与canvas所在的image plane平行的平面。
- 组成了视锥体，定义了场景中相机的可视范围。
- 相机与近裁截面的距离与焦距是完全无关的概念，不要混淆。
- *（与相机模型无关）定义了深度值的范围，与深度值精度高度相关。*
- 我们通常都会假定image plane在近裁截面上，也就是相机会在近裁截面上成像。这样的设定可以精简投影方程
  - 在这种情况下，Znear就表示相机与canvas之间的距离
图像大小 Type: 2 integers
- 渲染图像的尺寸，以像素数为单位
- 定义了resolution gate宽高比。
Gate Fit Type: enum
- 提供了当胶片尺寸宽高比与图像分辨率宽高比不同时的处理渲染，换种说法的话，也就是判断film gate与resolution gate要如何适配。
- 由Fill和Overscan两种选项。
Camer to World Type: 4x4 matrix
- 定义相机的位置与视线方向

有了以上参数，我们就可以计算出下列参数：

FOV Type: float
- 代表了相机捕获场景的视觉范围
- 由焦距和胶片尺寸计算而来
Canvas/Screen Window Type: 4 floats
- 表示canvas范围的四个坐标值，用与判断投影点是否可见
- 由canvas尺寸计算而来。
Film Gate Aspect Raio Type: float
- 决定了相机捕获的图像的形状
- 胶片宽度除以胶片高度即可得
Resolution Gate Aspect Raio Type: float
- 最终渲染的图片的宽高比，影响了NDC空间到栅格空间的变换
- 图片横向像素数除以图片纵向像素数

Computing the Canvas Coordinates

我们的思路很清晰：

通过焦距和胶片尺寸先计算出水平或竖直任意方向上的FOV
根据FOV和近裁截面与相机之间的距离Znear计算canvas尺寸

我们以水平方向为例，首先计算FOV：

\[\tan({\theta_V \over 2}) = {A \over B} = {\dfrac {\dfrac { \text{Film Aperture Height} } { 2 } } { \text{Focal Length} }}.\]

然后，根据相似三角形，我们可以表示出canvas的高度：

\[\begin{array}{l} \tan(\dfrac{\theta_V}{2}) = \dfrac{A}{B} = \dfrac{\dfrac{\text{Canvas Height} } { 2 } } { Z_{near} }, \\ \dfrac{\text{Canvas Height} } { 2 } = \tan(\dfrac{\theta_V}{2}) \times Z_{near},\\ \text{Canvas Height}= 2 \times {\tan(\dfrac{\theta_V}{2})} \times Z_{near}. \end{array}\]

将$\tan\left(\dfrac{\theta_V}{2}\right)$代入，可得：

\[\begin{array}{l} \text{Canvas Height}= 2 \times {\dfrac {\dfrac { \text{Film Aperture Height} } { 2 } } { \text{Focal Length} }} \times Z_{near}. \end{array}\]

计算canvas高度，实际上最终还是为了计算canvas的范围，我们可以得到表示canvas的上边界的Y值为：

\[\text{top} = {\dfrac {\dfrac { \text{Film Aperture Height} } { 2 } } { \text{Focal Length} }} \times Z_{near}\]

我们知道，canvas具有和胶片尺寸相同的宽高比，所以我们可以直接求出水平方向上的坐标值：

\[\text{right} = \dfrac {\dfrac { \text{Film Aperture Height} } { 2 } } { \text{Focal Length} } \times Z_{near} \times \dfrac{\text{Film Aperture Width}}{\text{Film Aperture Height}}\]

进一步简化，可得：

\[\text{right} = \dfrac {\dfrac { \text{Film Aperture Width} } { 2 } } { \text{Focal Length} } \times Z_{near}\]

我们通过代码来表述以上的计算过程：

  
int main(int argc, char **argv)
{
    float top = (filmApertureHeight / 2) / focalLength) * nearClippingPlane;
    float bottom = -top;
    float filmAspectRatio = filmApertureWidth / filmApertureHeight;
    float right = top * filmAspectRatio;
    // or 
    float right = (filmApertureWidth / 2) / focalLength) * nearClippingPlane;
    float left = -right;

    printf("Screen window bottom-left, top-right coordinates %f %f %f %f\n", bottom, left, top, right);
    ...
}

Rewrite Projection Function

现在，由于我们重新设定了canvas距离相机的距离，以及通过相机参数而计算canvas的尺寸，我们需要对计算像素坐标的函数有所调整：

此前，我们假设canvas距离相机一个单位长度的距离，而现在，canvas位于近裁截面上，即$\frac{P.y}{P.z}=\frac{P’.y}{Znear}$.我们需要在透视除法中乘以Znear
此前，我们使用的是硬编码的canvas尺寸，是直接在代码中进行定义，但现在我们需要根据相机的参数计算得到canvas的四个范围值，对应的参数需要调整
当判断像素坐标是否超出canvas范围时，我们可以使用计算好的canvas的四个范围值。

修改后的函数如下：

  
bool computePixelCoordinates(
    const Vec3f &pWorld,
    const Matrix44f &worldToCamera,
    const float &b,
    const float &l,
    const float &t,
    const float &r,
    const float &near,
    const uint32_t &imageWidth,
    const uint32_t &imageHeight,
    Vec2i &pRaster)
{
    Vec3f pCamera;
    worldToCamera.multVecMatrix(pWorld, pCamera);
    Vec2f pScreen;
    pScreen.x = pCamera.x / -pCamera.z * near;
    pScreen.y = pCamera.y / -pCamera.z * near;

    Vec2f pNDC;
    pNDC.x = (pScreen.x + r) / (2 * r);
    pNDC.y = (pScreen.y + t) / (2 * t);
    pRaster.x = static_cast<int>(pNDC.x * imageWidth);
    pRaster.y = static_cast<int>((1 - pNDC.y) * imageHeight);

    bool visible = true;
    if (pScreen.x < l || pScreen.x > r || pScreen.y < b || pScreen.y > t)
        visible = false;

    return visible;
}

When Resolution Gate and Film Gate Ratios Don’t Match

如果我们放任图像宽高比和胶片宽高比不一致，那么由胶片宽高比计算得到canvas宽高比就无法在栅格空间的变换中保留，最终会导致图片失真。所以我们在Fill模式和Overscan模式中选择一个，做出正确的处理。

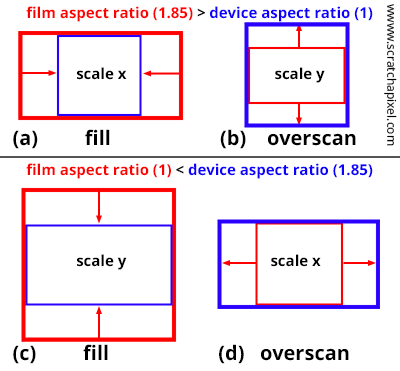
这两种模式其中也好区分：

Fill模式意味着缩小canvas：
- 在Film Gate大于Resolution Gate时，会将canvas的水平坐标缩小，也就是乘以Resolution Gate / Film Gate
- 在Resolution Gate大于Film Gate，会将canvas的竖直坐标缩小，也就是乘以Film Gate / Resolution Gate
Overscan模式意味着放大canvas：
- 在Film Gate大于Resolution Gate时，会将canvas的竖直坐标放大，也就是乘以Film Gate / Resolution Gate
- 在Resolution Gate大于Film Gate，会将canvas的竖水平坐标放大，也就是乘以Resolution Gate / Film Gate

代码如下：

  
float xscale = 1;
float yscale = 1;

switch (fitFilm) {
    default:
    case kFill:
        if (filmAspectRatio > deviceAspectRatio) {
            // Case 8a
            xscale = deviceAspectRatio / filmAspectRatio;
        } else {
            // Case 8c
            yscale = filmAspectRatio / deviceAspectRatio;
        }
        break;
    case kOverscan:
        if (filmAspectRatio > deviceAspectRatio) {
            // Case 8b
            yscale = filmAspectRatio / deviceAspectRatio;
        } else {
            // Case 8d
            xscale = deviceAspectRatio / filmAspectRatio;
        }
        break;
}

right *= xscale;
top *= yscale;
left = -right;
bottom = -top;

需要注意的是，不管是哪种模式，每次都只会处理canvas的一个方向的范围，所以我们需要在计算前设置大小为1的缩放值，也就是：

  
float xscale = 1;
float yscale = 1;

Graphics, Build A Soft Rasterizer

本文由作者按照 CC BY 4.0 进行授权