Surface Normals and Multiple Objects

发表于 2024/06/26 更新于 2024/12/16

作者 褴褛飞旋

21 分钟阅读

6.1 Shading with Surface Normals

我们需要先明确一点：在我们的光线追踪器中，并非所有法线都需要进行归一化，尤其是对于法线的方向来说。

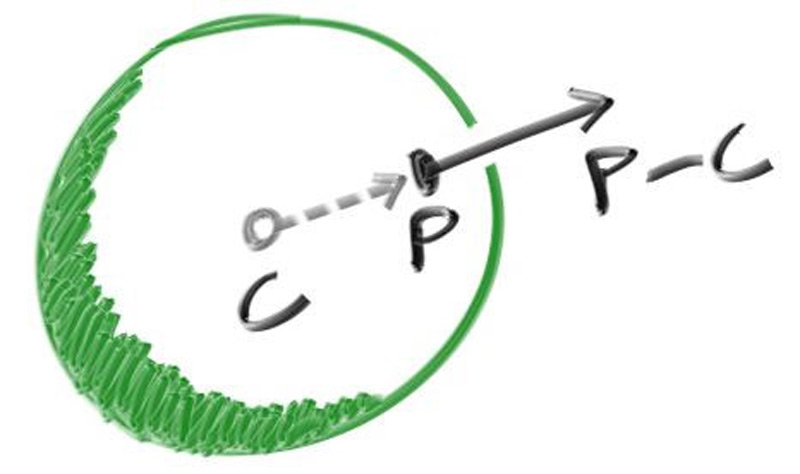
对于一个球体，法线就等于球面上一点减去球心得到的向量，如下图所示：

现在让我们将法线添加到到球体的着色计算中。因为目前我们的场景中还没有任何照明，我们暂时可以让球体的法线作为球体的颜色，具体的做法是，根据光线与球面的交点求出法线，然后对法线长度进行归一化。此时我们得到的法线的范围在【-1， 1】上，为了能够作为颜色值被写入到文件中，我们还需要做一次范围映射：

  
double hitSphere(const point3& center, double radius, const ray& r)
{
    vec3 oc = center - r.origin();
    double a = dot(r.direction(), r.direction());
    double b = dot(-2 * r.direction(), oc);
    double c = dot(oc, oc) - radius * radius;

    if (double discriminant = b * b - 4 * a * c; discriminant < 0)
    {
        return -1.0;
    }
    else
    {
        return (-b - sqrt(discriminant)) / (2.0 * a);
    }
}

color rayColor(const ray& r)
{
    // Objects in the scene
    if (double t = hitSphere(point3(0, 0, -1), 0.5, r); t > 0)
    {
        vec3 n = unitVectorLength(r.at(t) - point3(0, 0, -1));
        return (n + vec3(1, 1, 1)) * 0.5;
    }

    // Background
    vec3 unitDirection = unitVectorLength(r.direction());
    double a = (unitDirection.y() + 1.0) * 0.5;
    return color(1.0, 1.0, 1.0) * (1.0 - a) + color(0.5, 0.7, 1.0) * a;
}

我们得到的结果如下：

6.2 Simplifying the Ray-Sphere Intersection Code

由于光线-几何体测试是光线追踪中调用频率很高的函数，我们有必要对该函数进行优化，首先我们回顾一下光线-球体的相交测试的代码：

  
double hitSphere(const point3& center, double radius, const ray& r)
{
    vec3 oc = center - r.origin();
    double a = dot(r.direction(), r.direction());
    double b = dot(-2 * r.direction(), oc);
    double c = dot(oc, oc) - radius * radius;

    if (double discriminant = b * b - 4 * a * c; discriminant < 0)
    {
        return -1.0;
    }
    else
    {
        return (-b - sqrt(discriminant)) / (2.0 * a);
    }
}

我们已知，一个向量与自己点乘的结果等于该向量的平方长度。

其次，我们注意到b = -2.0 * dot(r.direction(), oc)，如果我们令b = -2 * h，其中h = dot(r.direction(), oc)，那我们就可以将整个求根公式中的2约去。

基于以上两点，我们得到优化后的代码：

  
double hitSphere(const point3& center, double radius, const ray& r)
{
    vec3 oc = center - r.origin();
    double a = dot(r.direction(), r.direction());
    double h = dot(r.direction(), oc);
    double c = dot(oc, oc) - radius * radius;

    if (double discriminant = h * h - a * c; discriminant < 0)
    {
        return -1.0;
    }
    else
    {
        return (h - sqrt(discriminant)) / a;
    }
}

6.3 An Abstraction for Hittable Objects

如果我们想要在场景中添加更多的球体，应该怎么处理呢？我们可以创建一个球体的数组，但更清晰有效的方法是实现一个抽象的类，用于表示任何可能被光线击中的东西。我们暂且将这个类命名为hittable

hittable抽象类需要有一个hit函数，并需要一个ray作为参数。几乎所有的光线追踪器都会为参数t设置一个范围[ t_min, t_max ]，只有t在这个范围内时，光线与几何体的碰撞才会被视为有效的。

还有一点需要我们提前确定，那就是我们是否需要计算出相交点的法线。考虑到光线可能会与场景中的多个几何体相交，所以为了减少不必要的运算，我们只需要计算与相机距离最近的相交点上的法线。

我们给出hittable抽象类的定义，同时我们将相交点处的几何信息存储在hitInfo类中：

  
#ifndef HITTABLE_H
#define HITTABLE_H

#include "ray.h"

class hitInfo
{
    public:
    point3 position;
    vec3 normal;
    double t;
};

class hittable
{
    public:
    virtual ~hittable() = default;

    virtual bool hit(const ray& r, double rayMinT, double rayMaxT, hitInfo& info) const = 0;
};

#endif

球体作为一个可以被光线击中的几何体，需要继承自hittable类，并单独存放在一个文件中。现在，我们可以将main.cpp中的hitSphere函数定义在sphere::hit中了。同时，因为我们已经创建了hitInfo类用于记录相交点处的相关信息，sphere::hit还需要执行相关赋值的语句，并根据光线是否会与球体相交返回一个bool值。

还有一点需要我们注意，在hittable::hit函数中，我们引入了一个范围，并设定只有当光线参数t位于这个范围中时，与几何体的相交才是有效的，为此，我们需要对根进行范围判定：

  
#ifndef SPHERE_H
#define SPHERE_H

#include "hittable.h"
#include "vec3.h"

class sphere final : public hittable
{
    public:
    sphere(const point3& center, double radius) : center(center), radius(fmax(0, radius)) {}

    bool hit(const ray& r, double rayMinT, double rayMaxT, hitInfo& info)
        const override
    {
        vec3 oc = center - r.origin();
        double a = dot(r.direction(), r.direction());
        double h = dot(r.direction(), oc);
        double c = dot(oc, oc) - radius * radius;

        double discriminant = h * h - a * c;
        if (discriminant < 0)
        {
            return false;
        }

        double sqrtD = sqrt(discriminant);
        double root = (h - sqrtD) / a;
        if (root <= rayMinT || root >= rayMaxT)
        {
            root = (h + sqrtD) / a;
            if (root <= rayMinT || root >= rayMaxT)
            {
                return false;
            }
        }

        info.position = r.at(root);
        info.normal = (info.position - center) / radius;
        info.t = root;

        return true;
    }

    private:
    point3 center;
    double radius;
};

#endif

6.4 Front Faces Versus Back Faces

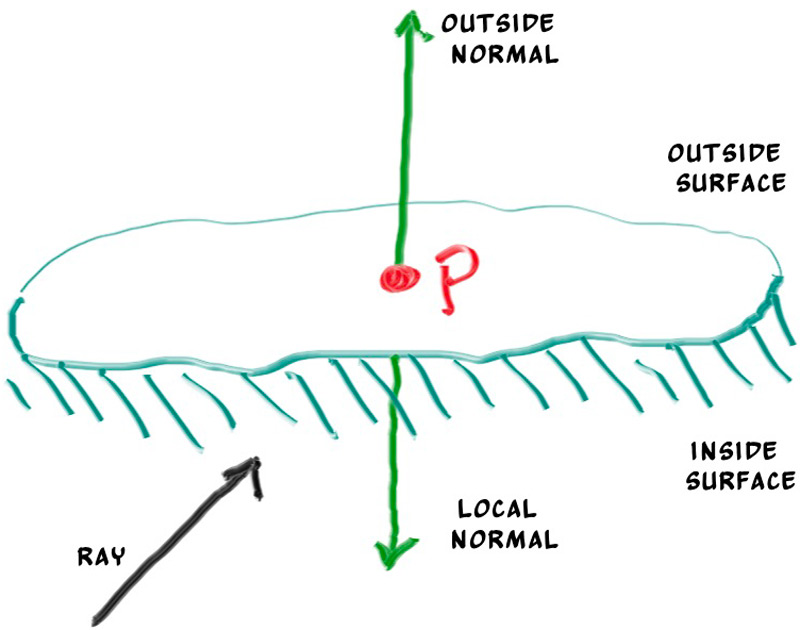
关于法线，我们还需要决定是否应该将法线设定为始终指向点外。在我们当前的代码中，我们计算得到的法线始终从球心指向相交点，也就是说，法线方向的计算方式与光线方向无关。

在这种计算方式下，如果光线从外侧与球体相交，那么法线指向光线方向相反的方向，如果光线从内侧与球体相交，那么法线与光线方向同向。当然，我们也可以设定法线始终与光线方向相反。

现在，我们需要从两个方式中选择一个，因为在某些情况下，还需要判断光线来自表面的哪一侧。比如双面纸上的文本内容，或者玻璃这种同时渲染内侧外侧的物体。

如果我们决定让法线始终指向外侧，那么当我们着色时，我们就需要判断光线在哪一侧。判断方法是比较法线与光线，如果方向相同，则光线在表面内侧，如果方向相反，则光线在表面外侧。而判断方向的一致性，我们可以通过点积来实现，即：

  
if (dot(ray_direction, outward_normal) > 0.0)
{
    // ray is inside the sphere
    ...
}
else
{
    // ray is outside the sphere
    ...
}

如果我们决定让法线始终指向与光线相反的方向，那我们就无需再计算点积来判断光线在表面哪一侧了。但是，我们需要将信息存储起来：

  
bool front_face;
if (dot(ray_direction, outward_normal) > 0.0)
{
    // ray is inside the sphere
    normal = -outward_normal;
    front_face = false;
}
else
{
    // ray is outside the sphere
    normal = outward_normal;
    front_face = true;
}

简而言之，两种方式的选择取决于在相交测试还是着色计算时确定表面的内外侧。在我们的这个系列博客中，材质类型多于几何类型，所以为了减少工作量，我们决定在几何体相交测试时进行判断，也就是说，我们会让法线始终指向与光线相反的方向。

我们将布尔值frontFace存储在hitInfo类中，并添加一个函数setNormalDirection用于判断当前面是否是正面，判断的依据是光线是否是从外侧与几何体表面相交，更多细节可以配合代码中的注释理解：

  
class hitInfo
{
    public:
    point3 position;
    vec3 normal; // normal vector has unit length
    double t;
    bool frontFace; // frontFace indicates from which side the ray hits the surface:
    // true means it hits from the outside.

    void setNormalDirection(const ray& r, const vec3& outsideNormal)
    {
        // outsideNormal is calculated in Function: hittable::hit(),
        // coming from hit point - sphere.center
        frontFace = dot(r.direction(), outsideNormal) < 0;
        normal = frontFace ? outsideNormal : -outsideNormal;
    }
};

最后，我们在sphere.h的hit()中调用setNormalDirection，完成对normal与frontFace的赋值：

  
info.position = r.at(root);
info.normal = (info.position - center) / radius;
vec3 outsideNormal = (info.position - center) / radius;
info.setNormalDirection(r, outsideNormal);
info.t = root;

6.5 A List of Hittable Objects

现在，我们已经构建了一个抽象的hittable对象了。接下来，我们需要添加一个类来存储hittable的列表：

  
#ifndef HITTABLE_LIST_H
#define HITTABLE_LIST_H

#include <memory>
#include <vector>

#include "hittable.h"

using std::make_shared;
using std::shared_ptr;

class hittableList final : public hittable
{
    public:
    std::vector<shared_ptr<hittable>> objects;

    hittableList() = default;
    explicit hittableList(const shared_ptr<hittable>& object) {add(object);}

    void clear() {objects.clear();}

    void add(const shared_ptr<hittable>& object)
    {
        objects.push_back(object);
    }

    bool hit(const ray& r, double rayMinT, double rayMaxT, hitInfo& info)
        const override
    {
        hitInfo tempInfo;
        bool hitAnything = false;
        double closestSoFar = rayMaxT;

        for (const shared_ptr<hittable>& object : objects)
        {
            if (object->hit(r, rayMinT, closestSoFar, tempInfo))
            {
                hitAnything = true;
                closestSoFar = tempInfo.t;
                info = tempInfo;
            }
        }

        return hitAnything;
    }
};

#endif

6.6 Some New C++ Features

在hittableList类中，我们使用了两个C++特性：vector和shared_ptr

shared_ptr是一个指向某个分配类型的指针，具有reference-counting的语义。每次将其值分配给另一个共享指针时，计数都会递增。当共享指针超出范围时（如在函数或者block的末尾），引用计数则会递减。计数归零后，将会安全地删除该对象。

通常来说，共享指针首先使用新分配的对象进行初始化，如下所示：

  
shared_ptr<double> double_ptr = make_shared<double>(0.37);
shared_ptr<vec3>   vec3_ptr   = make_shared<vec3>(1.414214, 2.718281, 1.618034);
shared_ptr<sphere> sphere_ptr = make_shared<sphere>(point3(0,0,0), 1.0);

我们的代码使用了共享指针，是因为它允许多个几何体共享一个公共实例，并且它让内存管理更加自动化且易于推理。

另一个特性是std::vector，是一个任意类型的类泛型数组集合，容量自由。

6.7 Common Constants and Utility Functions

在光线追踪器程序中，我们需要使用到一些数学常数，如一个无穷大的值，以及π。我们不妨将这些常量与通用的头文件、utility函数、std using放在一个头文件中：

  
#ifndef RAYTRACING_H
#define RAYTRACING_H

#include <cmath>
#include <iostream>
#include <limits>
#include <memory>

// C++ Std Usings
using std::make_shared;
using std::shared_ptr;
using std::sqrt;

// Constants
const double infinity = std::numeric_limits<double>::infinity();
constexpr double pi = 3.1415926535897932385;

// Utility Functions
inline double degreesToRadians(double degrees) {return degrees * pi / 180.0;}

// Common Headers
#include "ray.h"
#include "vec3.h"
#include "color.h"

#endif

因为我们会在main.cpp中包含rayTracing.h，那绝大部分其他头文件都可以默认这些定义是可用的，我们基于这点对我们的代码进行一定调整

  
#include <iostream>

  
#include "ray.h"

  
#include <memory>
#include <vector>

using std::make_shared;
using std::shared_ptr;

  
#include "vec3.h"

  
#include <cmath>
#include <iostream>

using std::sqrt;

以及我们重构的main.cpp：

  
#include "rayTracing.h"

#include "hittable.h"
#include "hittableList.h"
#include "sphere.h"

color rayColor(const ray& r, const hittable& world)
{
    if (hitInfo info; world.hit(r, 0, infinity, info))
    {
        return (info.normal + vec3(1, 1, 1)) * 0.5;
    }

    // Background
    vec3 unitDirection = unitVectorLength(r.direction());
    double a = (unitDirection.y() + 1.0) * 0.5;
    return color(1.0, 1.0, 1.0) * (1.0 - a) + color(0.5, 0.7, 1.0) * a;
}

int main()
{
    // Image------------------------------------------------------------
    double aspectRatio = 16.0 / 9.0;
    int imageWidth = 400;
    int imageHeight = static_cast<int>(imageWidth / aspectRatio);
    imageHeight = (imageHeight < 1) ? 1 : imageHeight;

    // World-----------------------------------------------------------
    hittableList world;
    world.add(make_shared<sphere>(point3(0,0,-1), 0.5));
    world.add(make_shared<sphere>(point3(0,-100.5,-1), 100));

    // Camera & Viewport------------------------------------------------
    point3 cameraCenter = point3(0, 0, 0);
    double focalLength = 1.0;
    double viewportHeight = 2.0;
    double viewportWidth = static_cast<double>(imageWidth) / imageHeight * viewportHeight;

    // calculate the vectors across the horizontal and down the viewport edges
    vec3 viewportU = vec3(viewportWidth, 0, 0);
    vec3 viewportV = vec3(0, -viewportHeight, 0);

    // calculate the horizontal and vertical delta vectors from pixel to pixel
    vec3 pixelDeltaU = viewportU / imageWidth;
    vec3 pixelDeltaV = viewportV / imageHeight;

    // calculate the location of the upper left pixel
    point3 viewportUpperLeft = cameraCenter - vec3(0, 0, focalLength) - viewportU / 2 - viewportV / 2;
    point3 firstPixelLocation = viewportUpperLeft + 0.5 * (pixelDeltaU + pixelDeltaV);

    // Render--------------------------------------------------------
    std::cout << "P3\n" << imageWidth << ' ' << imageHeight << "\n255\n";

    for (int j = 0; j < imageHeight; j++)
    {
        std::clog << "rScanlines remaining: " << (imageHeight - j) << "\n" << std::flush;

        for (int i = 0; i < imageWidth; i++)
        {
            point3 pixelCenter = firstPixelLocation + (i * pixelDeltaU) + (j * pixelDeltaV);
            vec3 rayDirection = pixelCenter - cameraCenter;
            ray r = ray(cameraCenter, rayDirection);

            color pixelColor = rayColor(r, world);
            writeColor(std::cout, pixelColor);
        }
    }

    std::clog << "rDone.              \n";
}

最终我们得到的结果是这样的：

6.8 An Interval Class

在继续之前，我们还需要实现一个用于管理区间的类

  
#ifndef INTERVAL_H
#define INTERVAL_H

class interval
{
public:
    double min, max;

    interval() : min(+infinity), max(-infinity) {} // default interval is empty

    interval(double min, double max) : min(min), max(max) {}

    [[nodiscard]] bool contains(double x) const
    {
        return min <= x && x <= max;
    }

    [[nodiscard]] bool surrounds(double x) const
    {
        return min < x && x < max;
    }

    static const interval empty, universe;
};

const interval interval::empty = interval(+infinity, -infinity);
const interval interval::universe = interval(-infinity, +infinity);

#endif

接下来，我们需要再次重构部分代码：

  
// rayTracing.h
#include "color.h"
#include "interval.h"
#include "ray.h"
#include "vec3.h"

  
class hittable  // NOLINT(cppcoreguidelines-special-member-functions)
{
public:
    virtual ~hittable() = default;

    virtual bool hit(const ray& r, double rayMinT, double rayMaxT, hitInfo& info) const = 0;   
    virtual bool hit(const ray& r, interval tInterval, hitInfo& info) const = 0;
};

  
class hittableList final : public hittable
{
public:
    ...

        bool hit(const ray& r, double rayMinT, double rayMaxT, hitInfo& info) const override
        bool hit(const ray& r, interval tInterval, hitInfo& info) const override
    {
        hitInfo tempInfo;
        bool hitAnything = false;
        double closestSoFar = rayMaxT;
        double closestSoFar = tInterval.max;

        for (const shared_ptr<hittable>& object : objects)
        {
            if (object->hit(r, rayMinT, closestSoFar, tempInfo))
                if (object->hit(r, interval(rayMinT, closestSoFar), tempInfo))
                {
                    hitAnything = true;
                    closestSoFar = tempInfo.t;
                    info = tempInfo;
                }
        }

        return hitAnything;
    }

    ...
};

  
class sphere final : public hittable
{
public:
    ...
        bool hit(const ray& r, double rayMinT, double rayMaxT, hitInfo& info)
        bool hit(const ray& r, interval tInterval, hitInfo& info)
        const override
    {
        ...
        double root = (h - sqrtD) / a;
        if (!tInterval.surrounds(root))
        {
            root = (h + sqrtD) / a;
            if (!tInterval.surrounds(root))
            {
                return false;
            }
        }
        ...
    }

    private:
    ...
};

  
color rayColor(const ray& r, const hittable& world)
{
    if (hitInfo info; world.hit(r, 0, infinity, info))
        if (hitInfo info; world.hit(r, interval(0, infinity), info))
        {
            return (info.normal + vec3(1, 1, 1)) * 0.5;
        }
    ...
}

Graphics, Ray Tracing In One Weekend

Ray Tracing

本文由作者按照 CC BY 4.0 进行授权