Quadrilaterals

发表于 2024/06/29 更新于 2024/12/16

作者 褴褛飞旋

18 分钟阅读

此前我们的渲染器只支持球体这一种primitive，现在是时候添加四边形了。

6.1 Defining the Quadrilateral

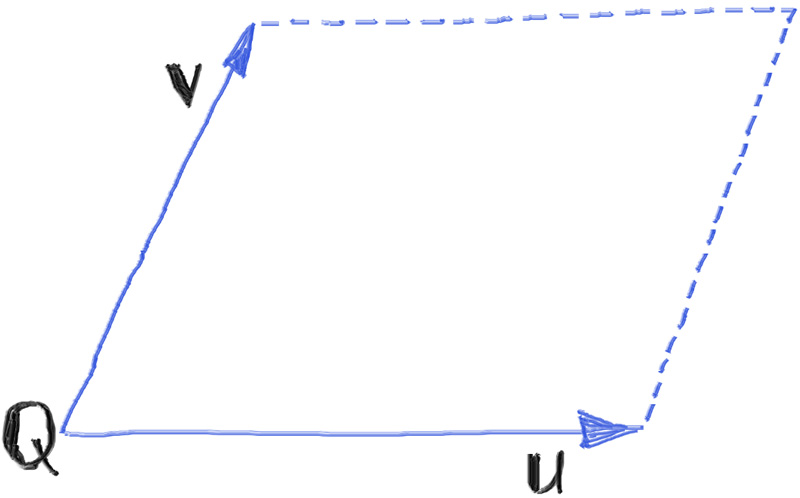
虽然在代码中我们会以quad来命名新的primitive，但从技术上来说，我们实际要实现的是平行四边形。我们通过以下三个参数定义平行四边形：

Q：起始的一角
u：表达平行四边形其中一条边的向量
v：表达平行四边形另一条边的向量

四边形是平的，所以如果四边形位于XY、YZ或ZX平面上，它们的AABB将在一个轴向上具有零厚度。这可能导致光线相交的数值问题。这里的数值问题主要是由于浮点数精度导致的相交检测失败等情况。

为了避免这些问题，我们可以在边界框的任何零厚度维度上增加一个小的填充。这样做不会改变四边形与其他几何体的实际相交情况，只是扩展了边界框，使其在所有维度上都有一个最小的正厚度，从而避免数值问题的出现。这样，边界框仍然是对四边形的一个粗略近似，但它变得更稳定、更可靠。

首先，我们需要添加一个函数，用于扩宽interval的范围：

  
class interval
{
public:
    ...

    interval expand(double delta) const
    {
        auto padding = delta / 2;
        return {min - padding, max + padding};
    }

    static const interval empty, universe;
};

接下来，我们来修改aabb类，避免出现某个轴向上AABB存在0厚度的情况：

  
class aabb
{
public:
	...

    aabb(const interval& x, const interval& y, const interval& z) : x(x), y(y), z(z)
    {
        padToMinimums();
    }

    aabb(const point3& a, const point3& b)
    {
        // here we treat a and b as extrema for the bounding box, and we sort them manually
        // thus we just dont require them to be particular minimum-maximum order
        x = a[0] <= b[0] ? interval(a[0], b[0]) : interval(b[0], a[0]);
        y = a[1] <= b[1] ? interval(a[1], b[1]) : interval(b[1], a[1]);
        z = a[2] <= b[2] ? interval(a[2], b[2]) : interval(b[2], a[2]);

        padToMinimums();
    }

	...

    static const aabb empty, universe;

private:

    void padToMinimums()
    {
        // adjust the AABB so that no side is narrower than some delta,
        // padding if necessary
        double delta = 0.0001;
        if (x.size() < delta) x = x.expand(delta);
        if (y.size() < delta) y = y.expand(delta);
        if (z.size() < delta) z = z.expand(delta);
    }
};

现在我们可以创建quad类，和sphere类一样，从hittable类中派生。我们可以留意下构造四边形AABB的方式，我们分别根据四边形对角线上的两个点构造一个AABB，然后再使用AABB的构造函数，将两个AABB合并为一个：

  
#ifndef QUAD_H
#define QUAD_H

#include "rayTracing.h"

#include "hittable.h"

class quad : public hittable
{
public:
    quad(const point3& Q, const vec3& u, const vec3& v, shared_ptr<material> material)
        : Q(Q), u(u), v(v), material(std::move(material))
    {
        setBoundingBox();
    }

    virtual void setBoundingBox()
    {
        // compute the bounding box of all four vertices
        auto bboxDiagonal1 = aabb(Q, Q + v + u);
        auto bboxDiagonal2 = aabb(Q + u, Q + v);
        bbox = aabb(bboxDiagonal1, bboxDiagonal2);
    }

    aabb boundingBox() const override {return bbox;}

    bool hit(const ray& r, interval tInterval, hitInfo& info) const override
    {
        return false; // to be implemented
    }

private:
    point3 Q;
    vec3 u, v;
    shared_ptr<material> material;
    aabb bbox;
};

#endif

6.2 Ray-Plane Intersection

我们解决光线与四边形相交检测的思路如下：

找到四边形所在的平面
判断光线是否与该平面相交
如果相交，我们再判断相交点是否在四边形内部

我们首先来解决第二个问题。实际上，光线与平面相交的思路与光线与球体相交的思路相同，甚至要更加简单。

在数学上，平面是所有满足以下这个隐式方程的点的集合：

\[Ax + By + Cz = D\]

其中，ABCD是常数，xyz是点的坐标。在计算机图形学中，我们也可以使用向量来理解这个式子：平面的法向量$n=(A,B,C)$与一个表示平面上一点的位置的向量$v=(x,y,z)$的点积：

\[\mathbf{n} \cdot \mathbf{v} = D\]

我们假设该点同样是光线与平面的交点，那么我们将光线的参数方程代入，就得到了一个关于t的一个等式：

\[t = \frac{D - \mathbf{n} \cdot \mathbf{P}}{\mathbf{n} \cdot \mathbf{d}}\]

解得t并代入到射线方程中，我们就得到了光线与平面的交点。需要注意的是，如果光线与平面平行，则等号右侧分式的分母为0。

实际上光线与三角形、圆形的相交问题也可以通过光线与平面的相交解决。

6.3 Finding the Plane That Contains a Given Quadrilateral

首先我们先明确一下问题：已知一个平行四边形其中一个顶点的位置，以及相邻两边的向量，求平行四边形所在的平面。

回想平面的隐式方程：$Ax+By+Cz=D$，其中ABC代表平面法线，我们可以通过求平行四边形两个邻边向量之间的叉积求得，即可得ABC。此外我们还已知平行四边形的一个顶点，该点毫无疑问在平面上，我们再代入到平面的方程中就可以求得D。

我们将平面的参数也添加到quad类：

  
class quad : public hittable
{
public:
    quad(const point3& Q, const vec3& u, const vec3& v, shared_ptr<material> material)
        : Q(Q), u(u), v(v), material(std::move(material))
    {
        // calculate the plane where the quad lies on
        vec3 n = cross(u, v);
        normal = unitVectorLength(n);
        D = dot(normal, Q);
            
        setBoundingBox();
    }

    ...

private:
    point3 Q;
    vec3 u, v;
    shared_ptr<material> material;
    aabb bbox;
    // plane parameters
    vec3 normal;
    double D;
};

接下来，我们补充完整quad::hit()，也就是使用前面我们推导的公式，计算出t，从而得到光线与平面的相交点：

  
class quad : public hittable
{
public:
    ...

    bool hit(const ray& r, interval tInterval, hitInfo& info) const override
    {
        double divisor = dot(normal, r.direction());
        // no hit if the ray is parallel to the plane
        if (fabs(divisor) < 1e-8) return false;

        // return false if the hit point parameter t is outside the ray interval
        double t = (D - dot(normal, r.origin())) / divisor;
        if (!tInterval.contains(t)) return false;

        point3 intersectionPoint = r.at(t);
        info.t = t;
        info.position = r.at(t);
        info.material = material;
        info.setNormalDirection(r, normal);

        return true;
    }

private:
	...
};

6.4 Orienting Points on The Plane

现在，我们能够已经能够计算出光线与平面的交点，但是这个交点可能在平面的任意位置上，可能在四边形外部，也可能在四边形内部。想要判断一个点是否在四边形中，并将平面的纹理坐标分配给交点，我们需要在平面上定位这个交点。

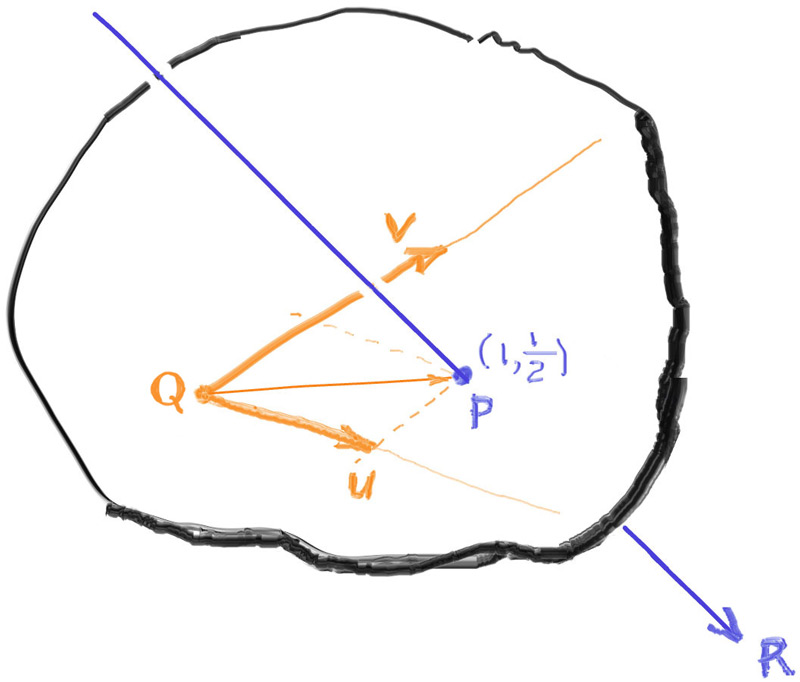
为了实现交点的定位，我们需要构建出平面的coordinate frame，从而能够在平面上定位任意一点。由于平面是2D的，我们只需要一个平面的原点Q与两个基向量u和v。通常而言，构建坐标系要求基向量是相互垂直的，但是这样做是为了能够将坐标系扩展到整个空间。但是对于我们此处的用途而言（定位平面上一点），我们只要求两个基向量不相互平行即可，实际上也就是四边形已知的两个向量u和v。

我们以上图为例，在平面的UV坐标系中，光线R与平面的交点P的坐标为(1, 1/2)。

而在更一般的情况中，我们需要找到两个标量，从而有

\[\mathbf{P} = \mathbf{Q} + \alpha \mathbf{u} + \beta \mathbf{v}\]

为了简化计算，我们引入一个权重向量w：

\[\mathbf{w} = \frac{\mathbf{n}}{\mathbf{n} \cdot (\mathbf{u} \times \mathbf{v})} = \frac{\mathbf{n}}{\mathbf{n} \cdot \mathbf{n}}\]

其中n是法向量，可以通过基向量的叉积得到。权重向量w是一个常量，对于给定的平面我们应该预先计算好：

  
class quad final : public hittable
{
public:
    quad(const point3& Q, const vec3& u, const vec3& v, shared_ptr<material> material)
        : Q(Q), u(u), v(v), material(std::move(material))
    {
        // calculate the plane where the quad lies on
        vec3 n = cross(u, v);
        normal = unitVectorLength(n);
        D = dot(normal, Q);
        w = n / dot(n, n);

        setBoundingBox();
    }
	...

private:
    point3 Q;
    vec3 u, v;
    vec3 w;
    shared_ptr<material> material;
    aabb bbox;
    // plane parameters
    vec3 normal;
    double D;
};

利用向量投影与叉积的性质，我们可以到两个标量的公式：

\[\displaylines{\alpha = \mathbf{w} \cdot (\mathbf{p} \times \mathbf{v}) \\ \beta = \mathbf{w} \cdot (\mathbf{u} \times \mathbf{p})}\]

6.5 Interior Testing of The Intersection Using UV Coordinates

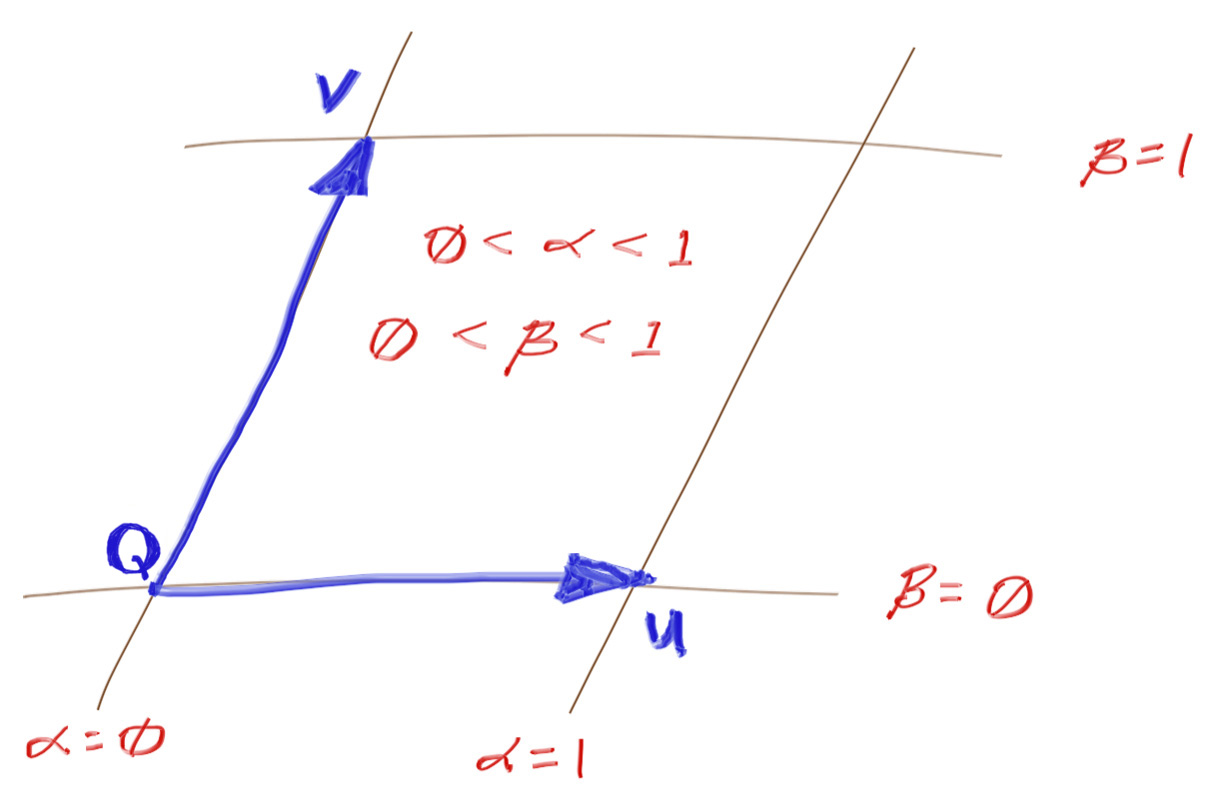
建立了平面的坐标系统，我们可以根据坐标值做平面进行划分，如下图所示：

也就是说，要判断平面上一点是否在四边形内，我们只需要进行如下的判定：

$0 \leq \alpha \leq 1$
$0 \leq \beta \leq 1$

我最初有些疑惑为什么是这样的判定条件。但是可以想一下，α和β就是依据四边形已知的两个边的向量计算得到的，当点的坐标超出[0, 1]的范围时，实际上也就是超出了四边形的范围。

这样一来，我们就可以将quad类补充完整了。为了代码的简洁，我们将判断平面上一点是否在四边形内的函数独立处理：

  
class quad : public hittable
{
public:
    ...

    bool hit(const ray& r, interval tInterval, hitInfo& info) const override
    {
        double divisor = dot(normal, r.direction());
        // no hit if the ray is parallel to the plane
        if (fabs(divisor) < 1e-8) return false;

        // return false if the hit point parameter t is outside the ray interval
        double t = (D - dot(normal, r.origin())) / divisor;
        if (!tInterval.contains(t)) return false;

        // determine the hit point lies within the planar shape using its plane coordinates
        point3 intersectionPoint = r.at(t);
        vec3 planarHitPointVector = intersectionPoint - Q;
        double alpha = dot(w, cross(planarHitPointVector, v));
        double beta = dot(w, cross(u, planarHitPointVector));

        if (!isInterior(alpha, beta, info))
            return false;
        
        info.t = t;
        info.position = intersectionPoint;
        info.material = material;
        info.setNormalDirection(r, normal);

        return true;
    }

    virtual bool isInterior(double a, double b, hitInfo& info) const
    {
        interval unitInterval = interval(0, 1);
        // given the hit point in plane coordinates,
        // return false if it is outside the primitive,
        // otherwise set the hit record UV coordinates and return true

        if (!unitInterval.contains(a) || !unitInterval.contains(b))
            return false;

        info.u = a;
        info.v = b;
        return true;
    }

private:
    ...
};

最后，我们再添加一个测试场景：

  
#include "rayTracing.h"

...
#include "material.h"
#include "quad.h"
#include "sphere.h"
#include "texture.h"

...

void quads()
{
    hittableList world;

    // Materials
    auto leftRed     = make_shared<lambertian>(color(1.0, 0.2, 0.2));
    auto backGreen   = make_shared<lambertian>(color(0.2, 1.0, 0.2));
    auto rightBlue   = make_shared<lambertian>(color(0.2, 0.2, 1.0));
    auto upperOrange = make_shared<lambertian>(color(1.0, 0.5, 0.0));
    auto lowerTeal   = make_shared<lambertian>(color(0.2, 0.8, 0.8));

    // Quads
    world.add(make_shared<quad>(point3(-3,-2, 5), vec3(0, 0,-4), vec3(0, 4, 0), leftRed));
    world.add(make_shared<quad>(point3(-2,-2, 0), vec3(4, 0, 0), vec3(0, 4, 0), backGreen));
    world.add(make_shared<quad>(point3( 3,-2, 1), vec3(0, 0, 4), vec3(0, 4, 0), rightBlue));
    world.add(make_shared<quad>(point3(-2, 3, 1), vec3(4, 0, 0), vec3(0, 0, 4), upperOrange));
    world.add(make_shared<quad>(point3(-2,-3, 5), vec3(4, 0, 0), vec3(0, 0,-4), lowerTeal));

    camera cam;

    cam.aspectRatio      = 1.0;
    cam.imageWidth       = 400;
    cam.samplesPerPixel = 100;
    cam.maxDepth         = 50;

    cam.verticalFOV = 80;
    cam.lookFrom = point3(0, 0, 9);
    cam.lookAt = point3(0, 0, 0);
    cam.viewUp = vec3(0,1,0);

    cam.defocusAngle = 0;

    cam.render(world);
}

int main()
{
    switch (5)
    {
        case 1: bouncingSphere(); break;
        case 2: checkeredSphere(); break;
        case 3: earth(); break;
        case 4: perlinSpheres(); break;
        case 5: quads(); break;
        default: ;
    }
}

渲染中。。。

6.6 Additional 2D Primitives

有注意到quad::setBoundingBox()与quad::isInterior()是虚函数吗？试想，如果我们可以通过坐标来判断平面上一点是否位于平行四边形内，则我们也可以使用这些坐标来确定点是否在其他2D的primitive内，例如三角形、椭圆、甚至是圆环。

我们在这里给出对应的代码，但是暂时不会将这些代码放在渲染器的正式版本的工程中：

  
class tri : public quad {
  public:
    tri(const point3& o, const vec3& aa, const vec3& ab, shared_ptr<material> m)
      : quad(o, aa, ab, m)
    {}

    virtual bool hit_ab(double a, double b, hit_record& rec) const override {
        if ((a < 0) || (b < 0) || (a + b > 1))
            return false;

        rec.u = a;
        rec.v = b;
        return true;
    }
};


class ellipse : public quad {
  public:
    ellipse(
        const point3& center, const vec3& side_A, const vec3& side_B, shared_ptr<material> m
    ) : quad(center, side_A, side_B, m)
    {}

    virtual void set_bounding_box() override {
        bbox = aabb(plane_origin - axis_A - axis_B, plane_origin + axis_A + axis_B).pad();
    }

    virtual bool hit_ab(double a, double b, hit_record& rec) const override {
        if ((a*a + b*b) > 1)
            return false;

        rec.u = a/2 + 0.5;
        rec.v = b/2 + 0.5;
        return true;
    }
};


class annulus : public quad {
  public:
    annulus(
        const point3& center, const vec3& side_A, const vec3& side_B, double _inner,
        shared_ptr<material> m)
      : quad(center, side_A, side_B, m), inner(_inner)
    {}

    virtual void set_bounding_box() override {
        bbox = aabb(plane_origin - axis_A - axis_B, plane_origin + axis_A + axis_B).pad();
    }

    virtual bool hit_ab(double a, double b, hit_record& rec) const override {
        auto center_dist = sqrt(a*a + b*b);
        if ((center_dist < inner) || (center_dist > 1))
            return false;

        rec.u = a/2 + 0.5;
        rec.v = b/2 + 0.5;
        return true;
    }

  private:
    double inner;
};

Graphics, Ray Tracing The Next Week

Ray Tracing

本文由作者按照 CC BY 4.0 进行授权