Instances
我们的康奈尔盒现在还有些空荡,所以让我们在房间中再添加两个方块。首先,我们需要通过6个quad来组成一个方块,我们可以创建一个函数,用于返回一个box
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class quad final: public hittable {...};
inline shared_ptr<hittableList> box(const point3& a, const point3& b, const shared_ptr<material>& material)
{
// return the 3D box (six sides) that contains the two opposite vertices a & b
auto sides = make_shared<hittableList>();
// construct the two opposite vertices with the minimum and maximum coordinates
auto min = point3(fmin(a.x(), b.x()), fmin(a.y(), b.y()), fmin(a.z(), b.z()));
auto max = point3(fmax(a.x(), b.x()), fmax(a.y(), b.y()), fmax(a.z(), b.z()));
auto dx = vec3(max.x() - min.x(), 0, 0);
auto dy = vec3(0, max.y() - min.y(), 0);
auto dz = vec3(0, 0, max.z() - min.z());
sides->add(make_shared<quad>(point3(min.x(), min.y(), max.z()), dx, dy, material)); // front
sides->add(make_shared<quad>(point3(max.x(), min.y(), max.z()), -dz, dy, material)); // right
sides->add(make_shared<quad>(point3(max.x(), min.y(), min.z()), -dx, dy, material)); // back
sides->add(make_shared<quad>(point3(min.x(), min.y(), min.z()), dz, dy, material)); // left
sides->add(make_shared<quad>(point3(min.x(), max.y(), max.z()), dx, -dz, material)); // top
sides->add(make_shared<quad>(point3(min.x(), min.y(), min.z()), dx, dz, material)); // bottom
return sides;
}
现在,我们将两个方块添加到康奈尔盒中:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void cornellBox()
{
...
// cornell box walls and light
world.add(make_shared<quad>(point3(555,0,0), vec3(0,555,0), vec3(0,0,555), green));
world.add(make_shared<quad>(point3(0,0,0), vec3(0,555,0), vec3(0,0,555), red));
world.add(make_shared<quad>(point3(343, 554, 332), vec3(-130,0,0), vec3(0,0,-105), light));
world.add(make_shared<quad>(point3(0,0,0), vec3(555,0,0), vec3(0,0,555), white));
world.add(make_shared<quad>(point3(555,555,555), vec3(-555,0,0), vec3(0,0,-555), white));
world.add(make_shared<quad>(point3(0,0,555), vec3(555,0,0), vec3(0,555,0), white));
// boxes in cornell box
world.add(box(point3(130, 0, 65), point3(295, 165, 230), white));
world.add(box(point3(265, 0, 295), point3(430, 330, 460), white));
camera cam;
...
}
渲染中。。。
只是,我们当前的渲染器还无法支持旋转两个方块。在光线追踪中,我们实现旋转的方式是instance。实例是放置在场景中的几何体的副本,一个实例与该物体的其他实例之间完全独立,可以任意的旋转与缩放。
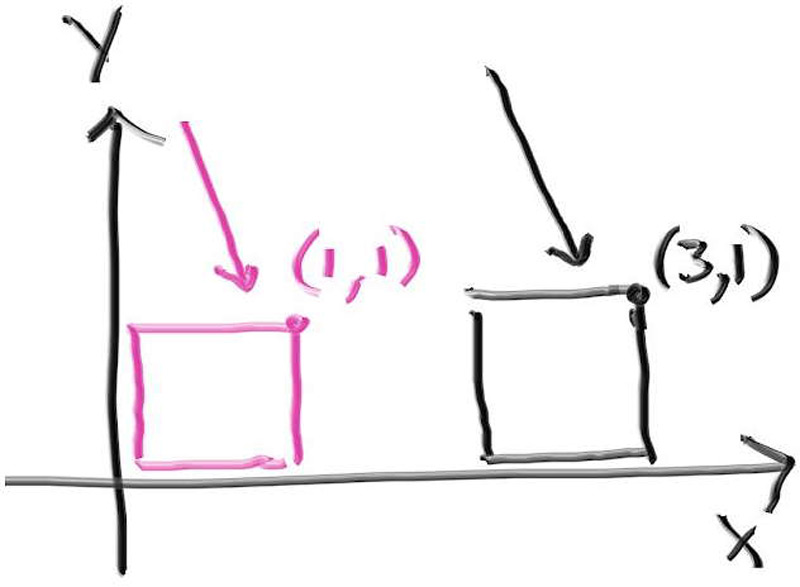
实际上我们并不需要移动场景中的物体,而是通过反向操作光线来实现旋转。例如,如果我们想平移一个几何体,我们可以通过在光线与几何体碰撞的计算过程中调整光线的位置来实现这个效果,而不需要真正移动几何体本身。这样做的好处是计算更加高效,因为我们只需要改变光线的参数,而不需要改变整个场景的几何体数据。如下图所示:
8.1 Instance Translation
我们再来清晰一下我们的思路:还是以上图为例,比如说我们想要把方块向右移动两个单位,我们的做法是不移动盒子,而是将光线向相反的方向移动,这样物体和光线的相对关系就等同于移动物体。我们用偏移后的光线计算是否与物体相交,如果存在相交,我们就将相交点进行相反的偏移。
我们将物体的移动作为一个新的类:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class hittable {...}
class translate : public hittable
{
public:
bool hit(const ray& r, interval tInterval, hitInfo& info) const override
{
// move the ray backwards by the offset
ray rayWithOffset(r.origin() - offset, r.direction(), r.time());
// determine whether an intersection exists along the offset ray
// and if so, where
if (!object->hit(rayWithOffset, tInterval, info))
return false;
// move the intersection point forwards by the offset
info.position += offset;
return true;
}
private:
shared_ptr<hittable> object;
vec3 offset;
};
除了移动相交点之外,我们还需要按照相同的思路处理AABB,也就是考虑到AABB的偏移值:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class translate final : public hittable
{
public:
translate(const shared_ptr<hittable>& object, const vec3& offset)
: object(object), offset(offset)
{
bbox = object->boundingBox() + offset;
}
bool hit(const ray& r, interval tInterval, hitInfo& info) const override {...}
aabb boundingBox() const override {return bbox;}
private:
shared_ptr<hittable> object;
vec3 offset;
aabb bbox;
};
但是当前的运算符+还不支持AABB与vec3之间的相加,让我们来添加实现对应的功能,这包含两部分,interval类的aabb类的修改:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
...
const interval interval::empty = interval(+infinity, -infinity);
const interval interval::universe = interval(-infinity, +infinity);
inline interval operator+(const interval &ival, double displacement)
{
return {ival.min + displacement, ival.max + displacement};
}
inline interval operator+(double displacement, const interval &ival)
{
return ival + displacement;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
...
const aabb aabb::empty = aabb(interval::empty, interval::empty, interval::empty);
const aabb aabb::universe = aabb(interval::universe, interval::universe, interval::universe);
inline aabb operator+(const aabb& bbox, const vec3& offset)
{
return {aabb(bbox.x + offset.x(), bbox.y + offset.y(), bbox.z + offset.z())};
}
inline aabb operator+(const vec3& offset, const aabb& bbox)
{
return bbox + offset;
}
8.2 Instance Rotation
我们暂时只先实现物体围绕Y轴的旋转
在translate类中,我们实现移动的步骤是:
- 将光线进行反向的偏移
- 用偏移后的光线进行相交测试,如果存在相交,则确定交点的位置
- 对交点进行偏移
如果我们从坐标系的角度来考虑,则上述步骤对应如下的思路:
- 将光线从世界空间变换到对象空间
- 在对象空间中判断是否存在交点
- 将交点变换到世界空间
我们可以使用同样的思路来处理旋转,只是我们需要注意,旋转同时也会改变法向量的坐标,从而改变反射与折射的方向。旋转时,坐标的计算公式是:
\[\displaylines{x' = \cos(\theta) \cdot x - \sin(\theta) \cdot z \\ z' = \sin(\theta) \cdot x + \cos(\theta) \cdot z}\]下面是完整的rotateY类:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
class rotateY final : public hittable
{
public:
rotateY(const shared_ptr<hittable>& object, double angle) : object(object)
{
double radians = degreesToRadians(angle);
sinTheta = sin(radians);
cosTheta = cos(radians);
bbox = object->boundingBox();
point3 min(infinity, infinity, infinity);
point3 max(-infinity, -infinity, -infinity);
for (int i = 0; i < 2; i++)
{
for (int j = 0; j < 2; j++)
{
for (int k = 0; k < 2; k++)
{
double x = i * bbox.x.max + (1 - i) * bbox.x.min;
double y = j * bbox.y.max + (1 - j) * bbox.y.min;
double z = k * bbox.z.max + (1 - k) * bbox.z.min;
double newX = cosTheta * x + sinTheta * z;
double newZ = -sinTheta * x + cosTheta * z;
vec3 tester(newX, y, newZ);
for (int c = 0; c < 3; c++)
{
min[c] = fmin(min[c], tester[c]);
max[c] = fmax(max[c], tester[c]);
}
}
}
}
bbox = aabb(min, max);
}
bool hit(const ray& r, interval tInterval, hitInfo& info) const override
{
// change the ray from world space to object space
point3 origin = r.origin();
vec3 direction = r.direction();
origin[0] = cosTheta * r.origin()[0] - sinTheta * r.origin()[2];
origin[2] = sinTheta * r.origin()[0] + cosTheta * r.origin()[2];
direction[0] = cosTheta * r.direction()[0] - sinTheta * r.direction()[2];
direction[2] = sinTheta * r.direction()[0] + cosTheta * r.direction()[2];
ray rayRotated(origin, direction, r.time());
// determine whether an intersection exists in object space
// and if so, where
if (!object->hit(rayRotated, tInterval, info)) return false;
// change the intersection point from object space to world space
point3 pos = info.position;
pos[0] = cosTheta * info.position[0] + sinTheta * info.position[2];
pos[2] = -sinTheta * info.position[0] + cosTheta * info.position[2];
// change the normal from object space to world space
vec3 normal = info.normal;
normal[0] = cosTheta * info.normal[0] + sinTheta * info.normal[2];
normal[2] = -sinTheta * info.normal[0] + cosTheta * info.normal[2];
info.position = pos;
info.normal = normal;
return true;
}
aabb boundingBox() const override { return bbox; }
private:
shared_ptr<hittable> object;
double sinTheta;
double cosTheta;
aabb bbox;
};
最后,我们给康奈尔盒中的两个方块添加位移和绕Y轴的旋转:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void cornellBox()
{
...
// boxes in cornell box
shared_ptr<hittable> box1 = box(point3(0,0,0), point3(165,330,165), white);
box1 = make_shared<rotateY>(box1, 15);
box1 = make_shared<translate>(box1, vec3(265,0,295));
world.add(box1);
shared_ptr<hittable> box2 = box(point3(0,0,0), point3(165,165,165), white);
box2 = make_shared<rotateY>(box2, -18);
box2 = make_shared<translate>(box2, vec3(130,0,65));
world.add(box2);
camera cam;
...
}
渲染中。。。