Diffuse Materials
现在,我们可以着手实现更为真实的材质了,首先是常见的漫反射材质
9.1 A Simple Diffuse Material
漫反射物体的特点是不发出自己的光,而是反射周围环境中的光。它们会把反射的光调制成自身的固有颜色。比如,如果一个红色的漫反射物体受到白光照射,它会反射出红色的光,因为它的固有颜色是红色。当光线照射到漫反射表面时,反射的方向是随机的,这意味着光线会以各种不同的角度反射出去。这个随机性使得漫反射表面看起来是均匀地散射光线,而不是像镜面那样产生清晰的反射。
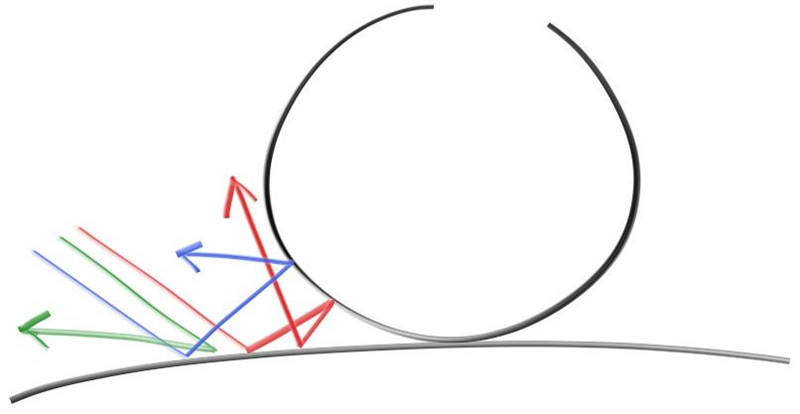
如果我们考虑两个漫反射表面之间的缝隙,并向其中发送三条光线,这三条光线在经过多次反射后会随机地改变方向。由于每条光线的反射方向都是随机的,这些光线的行为将是不同的。这种随机行为使得光线在缝隙内的路径变得难以预测,并且每条光线最终的去向和能量都会有所不同。这就是漫反射表面如何影响光线传输的一个重要特征。
除了被反射以外,光线还可能被吸收。任何让光线反射方向随机化的算法都会使表面看起来像哑光的。哑光表面没有光亮的反射点,因为光线被均匀地散射。所以,让我们先使用一种简单且直观的模型:光线在击中表面后,反射的方向是随机的,且在所有方向上均匀分布。
但是我们目前还没实现随机反射光线的功能,所以我们需要先在vec3类中添加一些新的函数,首先是生成任意的随机向量:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class vec3
{
public:
...
static vec3 randomUnitVector()
{
return {randomZeroToOne(), randomZeroToOne(), randomZeroToOne()};
}
static vec3 randomVector(double min, double max)
{
return {randomMinToMax(min, max), randomMinToMax(min, max),randomMinToMax(min, max)};
}
}
然后,我们需要弄清楚如何操控一个随机向量,使其结果只位于半球的表面。虽然有一些解析方法可能直接生成这样的随机向量,但这些方法通常难以理解和实现。在渲染领域中,我们最好避免使用这样的解析法。
为了简化这个过程,我们可以使用一个简单粗暴的方法:rejection sampling。在拒绝采样法中,我们会重复生成随机向量,检测该向量是否位于半球表面,如果不符合就继续生成新的变量,直到生成符合条件的向量。
有很多在半球上生成随机向量的方法,在我们的程序中,我们选择最简单的方式,即:
- 在单位球形中生成一个随机向量
- 归一化向量
- 如果向量在错误的半球内,则invert该向量
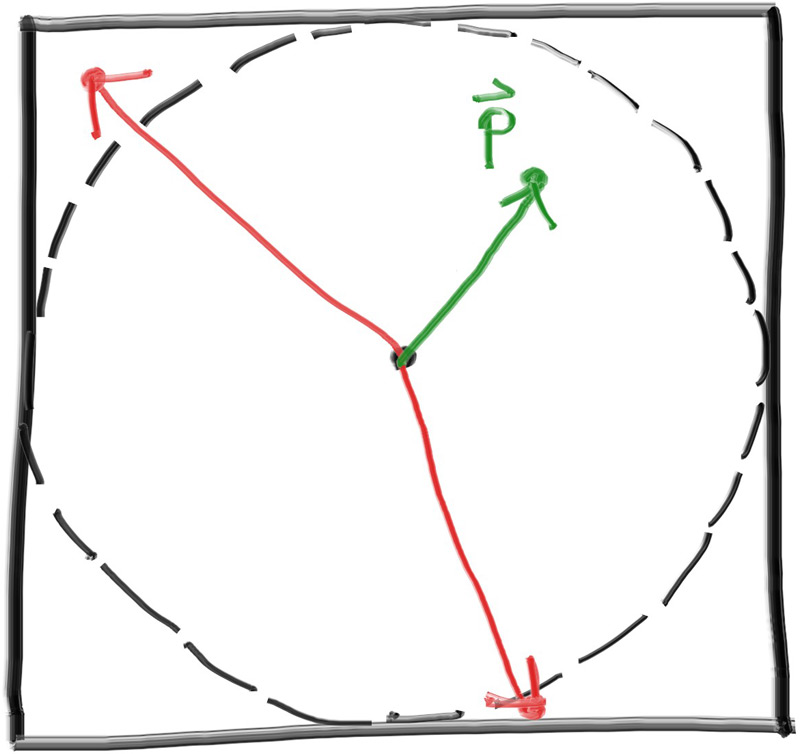
我们来逐步拆解。首先,我们使用vec3::randomVector()函数会在单位立方体中选择一个随机点,该点的xyz坐标均在[-1, 1]的范围内。然后再检测该点是否在单位球体内,如果没有,我们就舍弃该点,如下图所示:
对应的代码如下所示:
1
2
3
4
5
6
7
8
9
10
inline vec3 randomVectorOnUnitSphere()
{
while (true)
{
if (point3 p = vec3::randomVector(-1, 1); p.lengthSquared() < 1)
{
return p;
}
}
}
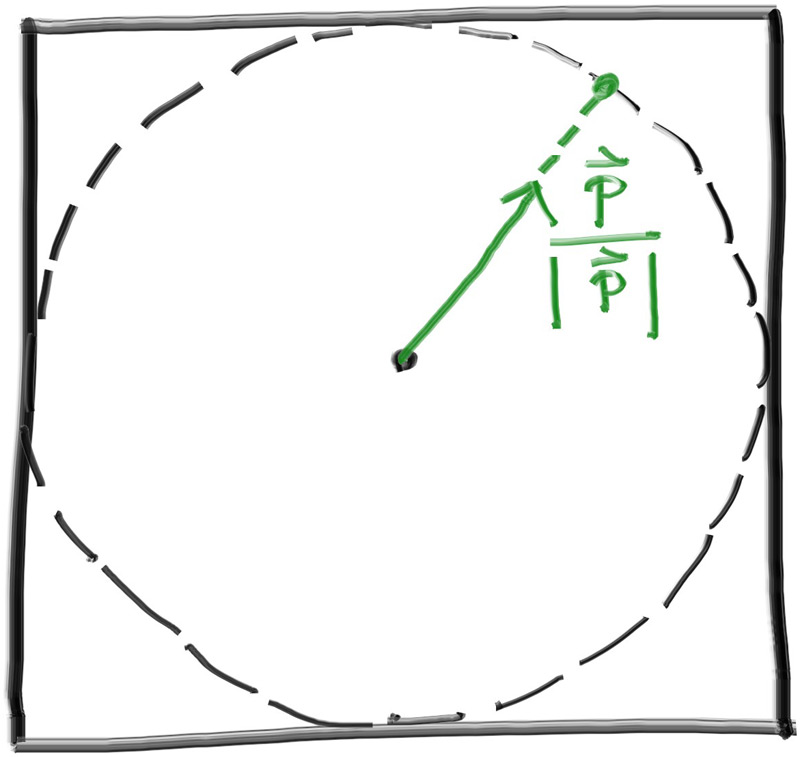
当我们生成了一个在单位球体内的向量,我们就可以通过归一化使得该点位于球体上,如下图所示:
对应代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
inline vec3 randomVectorOnUnitSphere()
{
while (true)
{
if (point3 p = vec3::randomVector(-1, 1); p.lengthSquared() < 1)
{
return p;
return unitVectorLength(p);
}
}
}
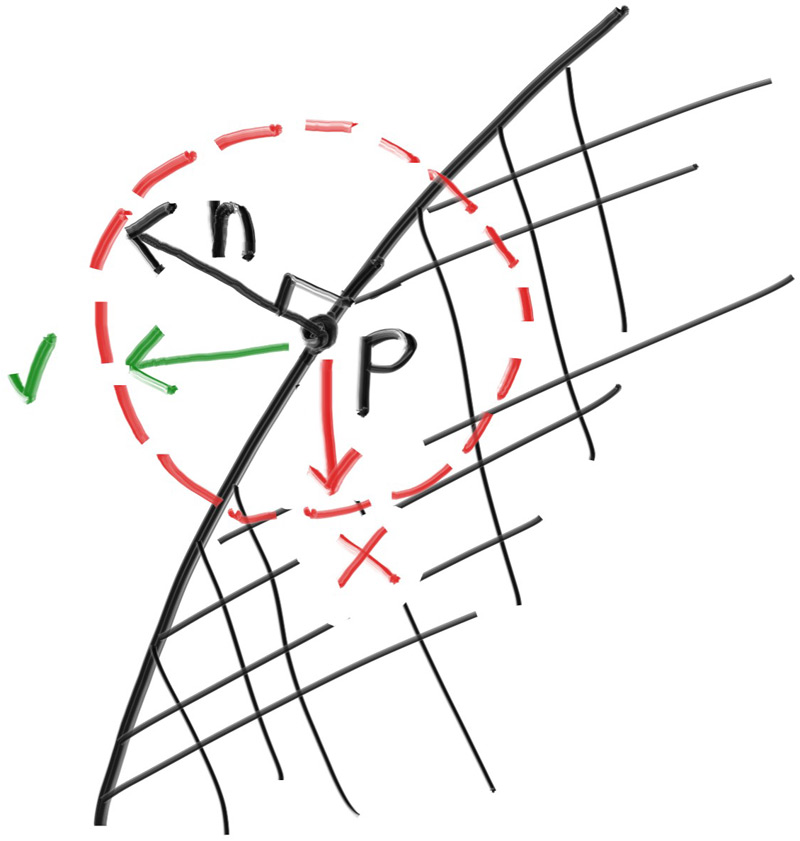
最后,我们还需要判断当前向量是否位于正确的半球上,我们可以通过该向量与表面法线的点乘判断,如下所示:
对应代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
inline vec3 randomVectorOnHemiSphere(const vec3& normal)
{
if (vec3 vectorOnUnitSphere = randomVectorOnUnitSphere(); dot(vectorOnUnitSphere, normal) > 0.0)
{
return vectorOnUnitSphere;
}
else
{
return -vectorOnUnitSphere;
}
}
如果光线从材料表面反射后,保持了材质的原始颜色的100%,我们称这个材料为白色。也就是说,白色材料不会吸收任何光线,它反射所有的入射光。如果光线从材料表面反射后,保持了其原始颜色的0%,我们称这个材料为黑色。也就是说,黑色材料吸收所有的入射光,不反射任何光线。
为了在场景中演示漫反射材质,我们让函数rayColor()在光线反射时返回颜色的50%,这意味着每次光线与材质交互时,颜色的亮度会减半。
1
2
3
4
5
6
7
8
9
10
11
static color rayColor(const ray& r, const hittable& world)
{
if (hitInfo info; world.hit(r, interval(0, infinity), info))
{
vec3 direction = randomVectorOnHemiSphere(info.normal);
return rayColor(ray(info.position, direction), world) * 0.5;
}
// Background
...
}
9.2 Limiting the Number of Child Rays
我们的代码中有一些潜在的问题,首先rayColor()是一个递归函数,但是我们并没有设置一个递归中止的条件。我们知道,当光线不再击中任何物体时,递归就应该结束了。此外,在一些复杂的场景下,递归深度可能会导致栈溢出。
所以,我们需要限制最大的递归次数,在最大递归深度时,返回黑色,也就是没有光照结果:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
[[nodiscard]]
static color rayColor(const ray& r, int depth, const hittable& world)
{
// if we've exceeded the ray bounce limit, no more light is gathered
if (depth <= 0)
{
return {0.0, 0.0, 0.0};
}
if (hitInfo info; world.hit(r, interval(0, infinity), info))
{
vec3 direction = randomVectorOnHemiSphere(info.normal);
return rayColor(ray(info.position, direction), depth - 1, world) * 0.5;
}
// Background
...
}
对应的,我们需要给camera类添加一个成员变量maxDepth,作为最大迭代次数,并且在第一次调用rayColor()时传递给函数
1
2
3
4
5
6
7
8
9
10
11
12
13
class camera
{
public:
...
int maxDepth = 10; // Maxmium number of ray bounces into scene
void render(const hittable& world)
{
...
pixelColor += rayColor(r, maxDepth, wolrd);
...
}
}
在我们的测试场景中,我们将最大迭代次数设置为50
1
cam.maxDepth = 50;
由于我们场景比较简单,当我们再次渲染时,可能效果并不明显
9.3 Fixing Shadow Acne
光线与表面相交点时可能遇到的一个微妙的错误。光线会尝试精确计算与表面相交的点,但由于浮点数舍入误差,计算出的相交点可能会稍微有些偏差。这意味着从表面随机散射出的下一条光线的起点不太可能与表面完全齐平。它可能会略高于或略低于表面。如果光线的起点略低于表面,那么它可能会再次与该表面相交,从而在t=0.00000001(或由命中函数给出的任何浮点近似值)处找到最近的表面。解决这个问题的最简单方法是忽略那些非常接近计算出的相交点的命中点:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
color ray_color (const ray& r, int depth, const hittable& world) const
{
// if we've exceeded the ray bounce limit, no more light is gathered
if (depth <= 0)
return color(0, 0, 0);
hit_record rec;
if (world.hit(r, interval(0, infinity), rec))
if (world.hit(r, interval(0.001, infinity), rec))
{
vec3 direction = random_on_hemisphere(rec.normal);
return 0.5 * ray_color(ray(rec.p, direction), depth - 1, world);
}
vec3 unit_direction = unit_vector(r.direction());
auto a = 0.5*(unit_direction.y() + 1.0);
return (1.0-a) * color(1.0, 1.0, 1.0) + a * color(0.5, 0.7, 1.0);
}
这样,shadow acne的问题就会得到很大程度的改善:
9.4 True Lambertian Reflection
在半球上均匀地散布反射光线会带给我们一个不错的漫反射模型,但还有更进一步的空间。真实的漫反射物体遵循一个更为精准的模型:Lambertian分布。
兰伯特分布模型中,反射光线的散布与cos(ϕ)的比例相关,其中ϕ表示反射光线与表面法线之间的角度。也就是说,反射光线更倾向于散布在靠近表面法线的方向上。相比于我们当前所使用的分布模型,兰伯特分布是非均匀的,在模拟现实世界中的材质反射上有更好的效果。
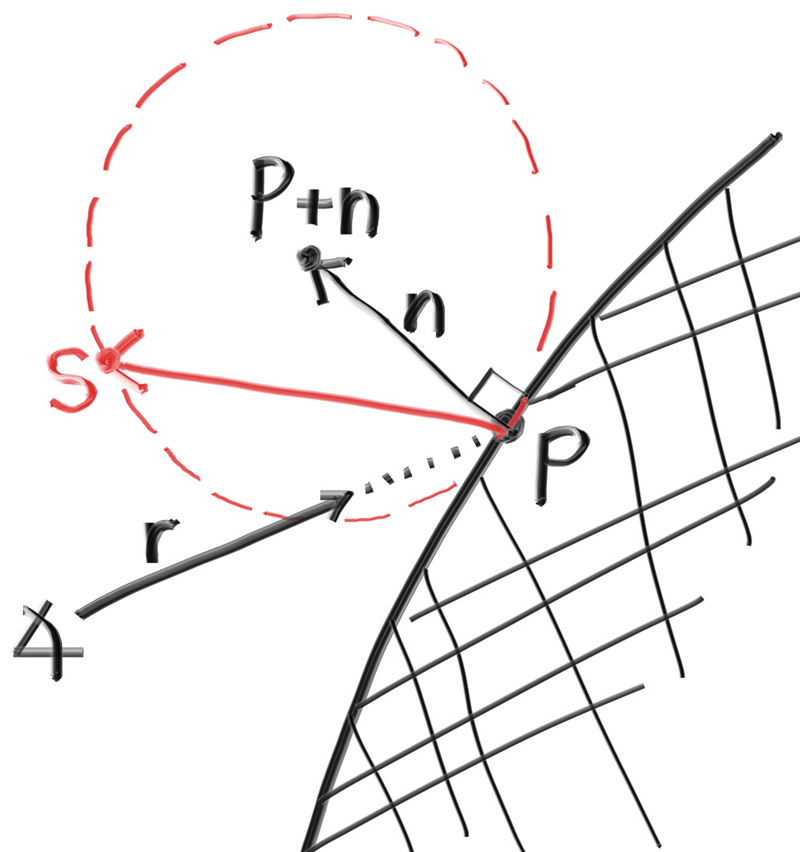
我们可以通过给法线向量增加一个随机单位向量来实现兰伯特散布。具体来说,我们将表面上的相交点命名为点P,表面法线命名为n。在相交点的位置上,表面有内外两侧,所以对于任意相交点来说,只会有两个独一无二的与表面相切的单位球体。这两个单位球体会沿着法线向量移动一个单位长度,如下图所示:
在我们的渲染器中,我们想要选择相对于表面,与光线原点在同一侧的球体,然后在球体上任选一点S,然后构建一条新的光线S-P,这个光线就是用于递归的新光线。对应的代码相当简单:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
[[nodiscard]]
static color rayColor(const ray& r, int depth, const hittable& world)
{
// if we've exceeded the ray bounce limit, no more light is gathered
if (depth <= 0)
{
return {0.0, 0.0, 0.0};
}
if (hitInfo info; world.hit(r, interval(0.001, infinity), info))
{
vec3 direction = randomVectorOnHemiSphere(info.normal);
vec3 direction = info.normal + randomVectorOnUnitSphere();
return rayColor(ray(info.position, direction), depth - 1, world) * 0.5;
}
// Background
...
}
使用新的分布模型得到的结果如下图所示:
我们可能难以分辨两种分布模型这个简单场景中的区别,但是我们应该不难注意到有两个很重要的点:
- 阴影变得更加明显
- 球体会从天空中获取到蓝色
这两种变换都是由于反射光线更多地向表面法线上散射造成的。
9.5 Using Gamma Correction for a Accurate Color Intensity
我们当前的渲染结果看起来很暗,但是球体仅仅会从每次光线反射中吸收50%的能量,在现实场景中,这些球体应该看起来更亮一些。出现这个问题的原因是,几乎所有的计算机程序都会假定,在图片被写入到图片文件之前,都会经过伽马矫正的处理。也就是说,0到1的值在被存储为字节之前,会得到某些转换。我们称没有被伽马矫正的图片在线性空间下,而经过处理的图片位于伽马空间下。当我们使用图片浏览器查看我们的渲染结果是,它会假设我们的图片处于伽马空间下,这就能解释为什么我们的图片看起来会很暗。
将图片转换到伽马空间下的原因很多,但我们的博客暂时不做解释,我们只需要知道,渲染结果应该得到伽马矫正就行。转换的过程与颜色相关,所以我们需要修改color.h中的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
inline double linear_to_gamma(double linear_component)
{
if (linear_component > 0)
return sqrt(linear_component);
return 0;
}
void write_color(std::ostream& out, const color& pixel_color)
{
auto r = pixel_color.x();
auto g = pixel_color.y();
auto b = pixel_color.z();
// apply a linear to gamma transform for gamma 2
r = linear_to_gamma(r);
g = linear_to_gamma(g);
b = linear_to_gamma(b);
// Translate the [0,1] component values to the byte range [0, 255]
static const interval intensity(0.000, 0.999);
int rbyte = int(256 * intensity.clamp(r));
int gbyte = int(256 * intensity.clamp(g));
int bbyte = int(256 * intensity.clamp(b));
// Write out the pixel color components
out << rbyte << ' ' << gbyte << ' ' << bbyte << '\n';
}
下面是经过伽马矫正后的渲染结果: