Dielectrics
像水、玻璃和钻石这样的透明材料是电介质。当光线照射到它们时,会分裂成反射光线和折射(透射)光线。我们将通过随机选择反射或折射来处理这一现象,每次交互只生成一条散射光线。
折射光线在从环境进入材料本身时会发生弯曲(例如玻璃或水)。这就是为什么当铅笔部分插入水中时会看起来弯曲。折射光线弯曲的程度由材料的折射率决定。通常,这是一个描述从真空进入材料时光线弯曲程度的单一值。玻璃的折射率大约在1.5到1.7之间,钻石大约是2.4,空气的折射率则是1.000293。
当一种透明材料嵌入到另一种透明材料中时,可以用相对折射率来描述折射现象:即物体材料的折射率除以周围材料的折射率。例如,如果你想渲染水下的玻璃球,那么玻璃球的有效折射率是1.125。这个值是玻璃的折射率(1.5)除以水的折射率(1.333)得到的。
11.1 Snell’s Law
Snell定律为我们描述了折射现象:
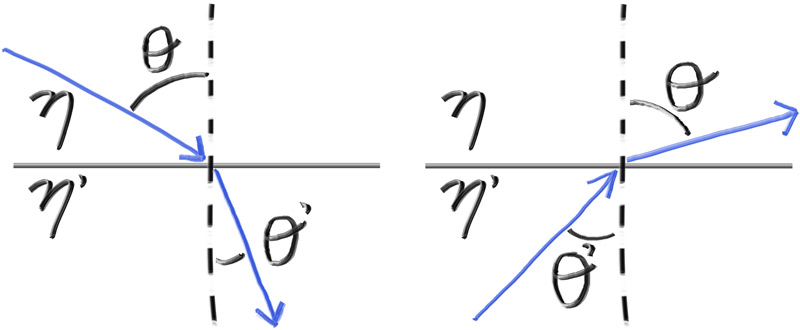
\[\eta \cdot \sin\theta = \eta' \cdot \sin\theta'\]其中,θ与θ′是光线与法线之间的夹角,η和η′则表示反射率,如下图所示:
所以,我们可以利用Snell定律求出折射角度,也就是
\[\sin\theta' = \frac{\eta}{\eta'} \cdot \sin\theta\]我们将表面内侧上的法线命名为n′,折射光线记作R′,两个向量之间的夹角也就是θ′。我们可以将R′分为两个向量,两个向量分别与法线n′垂直与平行,也就是:
\(\mathbf{R'} = \mathbf{R'}_{\bot} + \mathbf{R'}_{\parallel}\) 其中R′⊥与R′∥可以通过下面的式子计算求出,而cosθ则可以通过入射光线与表面外侧的法线的点积计算得到。:
\[\displaylines{\mathbf{R'}_{\bot} = \frac{\eta}{\eta'} (\mathbf{R} + \cos\theta \mathbf{n}) \\ \mathbf{R'}_{\parallel} = -\sqrt{1 - |\mathbf{R'}_{\bot}|^2} \mathbf{n}}\]具体的证明步骤并不是本篇博客的重点
最终我们可以将计算折射光线的代码整理出来:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
...
inline vec3 reflect(const vec3& v, const vec3& n)
{
...
}
inline vec3 refract(const vec3& rayIncoming, const vec3& n, double relativeR)
{
double cosTheta = fmin(dot(-rayIncoming, n), 1.0);
vec3 perpVector = relativeR * (rayIncoming + cosTheta * n);
vec3 paraVector = -sqrt(fabs(1.0 - perpVector.lengthSquared())) * n;
return perpVector + paraVector;
}
有了折射函数,我们就可以实现一个会折射所有入射光线的电介质材质了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
...
class metal final : public material
{
...
}
class dielectric final : public material
{
public:
explicit dielectric(double refractionIndex) : refractionIndex(refractionIndex) {}
bool scatter(const ray& rayIncoming, const hitInfo& info, color& attenuation, ray& rayScattered)
const override
{
attenuation = {1.0, 1.0, 1.0};
double relativeR = info.frontFace ? (1.0 / refractionIndex) : refractionIndex;
vec3 unitIncomingDirection = unitVectorLength(rayIncoming.direction());
vec3 direction = refract(unitIncomingDirection,info.normal, relativeR);
rayScattered = ray(info.position, direction);
return true;
}
private:
double refractionIndex;
};
需要注意的是,对于电介质材质来说,albedo始终为1,因为像玻璃这种物体我们假定并不会吸收任何光线。
我们可以将测试场景中左侧的球体改为电介质材质:
1
2
3
4
auto groundMaterial = make_shared<lambertian>(color(0.8, 0.8, 0.0));
auto centerSphereMaterial = make_shared<lambertian>(color(0.1, 0.2, 0.5));
auto leftSphereMaterial = make_shared<dielectric>(1.50);
auto rightSphereMaterial = make_shared<metal>(color(0.8, 0.6, 0.2), 1.0);
渲染中。。。
11.2 Total Internal Reflection
在折射现象中,我们还需要考虑到一些无法使用Snell定律的光线角度。当光线以一定的掠视角度进入折射率较低的材质时,它会以大于90度的角度折射。我们将这种现象称为全内反射Total Internal Reflection,当光从一种密介质(如水或玻璃)传播到另一种光疏介质(如空气)时,入射角大于某个临界角(critical angle),光线不会再折射出界面,而是全部反射回原来的介质中。我们可以使用Snell定律推导一下:
\[\sin\theta' = \frac{\eta}{\eta'} \cdot \sin\theta\]假设光线从玻璃射到到空气中,我们将反射率代入:
\[\sin\theta' = \frac{1.5}{1.0} \cdot \sin\theta\]然而,sin函数的最大值为1,所以上面这个式子是无解的,也就是说,我们可以通过判断等式右侧的值是否大于1来判断当前光线能否被折射,如果光线不能被折射,只能被反射:
1
2
3
4
5
6
7
8
9
if (relativeR * sinTheta > 1.0)
{
// must reflect
...
}
else
{
// can refract
}
我们已知cosθ,就可以通过三角函数计算出sinθ,这样我们就可以进一步完善了dielectric类了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class dielectric final : public material
{
public:
explicit dielectric(double refractionIndex) : refractionIndex(refractionIndex) {}
bool scatter(const ray& rayIncoming, const hitInfo& info, color& attenuation, ray& rayScattered)
const override
{
attenuation = {1.0, 1.0, 1.0};
double relativeR = info.frontFace ? (1.0 / refractionIndex) : refractionIndex;
vec3 unitIncomingDirection = unitVectorLength(rayIncoming.direction());
double cosTheta = fmin(dot(-unitIncomingDirection, info.normal), 1);
double sinTheta = sqrt(1.0 - cosTheta * cosTheta);
bool cannotRefract = relativeR * sinTheta > 1.0;
vec3 direction;
if (cannotRefract)
{
direction = reflect(unitIncomingDirection, info.normal);
}
else
{
direction = refract(unitIncomingDirection,info.normal, relativeR);
}
rayScattered = ray(info.position, direction);
return true;
}
private:
double refractionIndex;
};
为了展示全内反射的效果,我们修改测试场景中左侧球体的材质为电介质,同时将refractionIndex设置为1.00 / 1.33,表示球体的材质为空气(折射率1.0),而场景所在的世界是被水(折射率1.33)浸没的
1
2
3
4
auto groundMaterial = make_shared<lambertian>(color(0.8, 0.8, 0.0));
auto centerSphereMaterial = make_shared<lambertian>(color(0.1, 0.2, 0.5));
auto leftSphereMaterial = make_shared<dielectric>(1.0 / 1.33);
auto rightSphereMaterial = make_shared<metal>(color(0.8, 0.6, 0.2), 1.0);
渲染中。。。
11.3 Schlick Approximation
现实世界中的玻璃的反射率会根据观察角度而变化,当我们从一个较低的角度观察玻璃,会发现玻璃呈现出镜面的效果。有一个等式可以描述这个现象,但渲染领域的惯例是使用Chritophe Schlic的近似方法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class dielectric final : public material
{
public:
explicit dielectric(double refractionIndex) : refractionIndex(refractionIndex) {}
bool scatter(const ray& rayIncoming, const hitInfo& info, color& attenuation, ray& rayScattered)
const override
{
attenuation = {1.0, 1.0, 1.0};
double relativeR = info.frontFace ? (1.0 / refractionIndex) : refractionIndex;
vec3 unitIncomingDirection = unitVectorLength(rayIncoming.direction());
double cosTheta = fmin(dot(-unitIncomingDirection, info.normal), 1);
double sinTheta = sqrt(1.0 - cosTheta * cosTheta);
bool cannotRefract = relativeR * sinTheta > 1.0;
vec3 direction;
if (cannotRefract || reflectance(cosTheta, relativeR) > randomZeroToOne())
{
direction = reflect(unitIncomingDirection, info.normal);
}
else
{
direction = refract(unitIncomingDirection,info.normal, relativeR);
}
rayScattered = ray(info.position, direction);
return true;
}
private:
double refractionIndex;
static double reflectance(double cosine, double refractionIndex)
{
// use Schlick's approximation for reflectance
double r = (1 - refractionIndex) / (1 + refractionIndex);
r = r * r;
return r + (1 - r) * pow((1 - cosine), 5);
}
};
11.4 Modeling a Hollow Glass Sphere
现在让我们在测试场景中添加一个空心玻璃球,场景中的光线在击中这个球体后,会首先发生折射,然后折射光线会再次击中玻璃球内部中的以空气为材质的球体,然后发生第二次折射,折射后的光线会穿过空气,从玻璃材质内侧击中表面,折射回来,然后再击中外球体的内表面,最终折射到场景中的空气里。
我们修改构建场景的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
...
auto groundMaterial = make_shared<lambertian>(color(0.8, 0.8, 0.0));
auto centerSphereMaterial = make_shared<lambertian>(color(0.1, 0.2, 0.5));
auto leftSphereMaterial = make_shared<dielectric>(1.50);
auto bubbleMaterial = make_shared<dielectric>(1.00 / 1.50);
auto rightSphereMaterial = make_shared<metal>(color(0.8, 0.6, 0.2), 1.0);
world.add(make_shared<sphere>(point3(0.0, -100.5, -1.0), 100.0, groundMaterial));
world.add(make_shared<sphere>(point3(0.0, 0.0, -1.2), 0.5, centerSphereMaterial));
world.add(make_shared<sphere>(point3(-1.0, 0.0, -1.0), 0.5, leftSphereMaterial));
world.add(make_shared<sphere>(point3(-1.0, 0.0, -1.0), 0.4, bubbleMaterial));
world.add(make_shared<sphere>(point3(1.0, 0.0, -1.0), 0.5, rightSphereMaterial));
...
渲染中。。。